题目内容
A.(选修模块3-3)
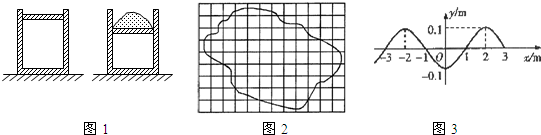
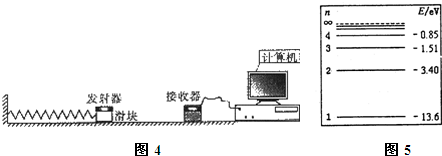
(1)一定质量的理想气体发生等容变化,下列图象正确的是 .
(2)如图所示,某同学在环境温度稳定的实验室里做热学小实验,用手指堵住注射器前端小孔,这时注射器内就封闭了一定质量的空气(可看成理想气体).若该同学往里缓慢地推活塞(如图甲),气体的压强 (选填“增大”或“减小”).若该同学缓慢推进活塞过程中做功为W1;然后将活塞缓慢稍稍拉出一些(如图乙),此过程中做功为W2,则全过程中注射器内空气的内能增加量△U= .

(3)用油膜法可粗略测出阿伏加德罗常数,把密度ρ=0.8×103 kg/m3的某种油,用滴管滴出一滴油在水面上形成油膜,已知这滴油的体积V=0.5×10-3 cm3,形成的油膜的面积S=0.7m2,油的摩尔质量Ml=0.09kg/mol.若把油膜看成单分子层,每个油分子看成球形,那么:
(a)油分子的直径为多大?
(b)由以上数据可测出的阿伏加德罗常数大约为多少?(保留一位有效数字)
(1)一定质量的理想气体发生等容变化,下列图象正确的是
(2)如图所示,某同学在环境温度稳定的实验室里做热学小实验,用手指堵住注射器前端小孔,这时注射器内就封闭了一定质量的空气(可看成理想气体).若该同学往里缓慢地推活塞(如图甲),气体的压强

(3)用油膜法可粗略测出阿伏加德罗常数,把密度ρ=0.8×103 kg/m3的某种油,用滴管滴出一滴油在水面上形成油膜,已知这滴油的体积V=0.5×10-3 cm3,形成的油膜的面积S=0.7m2,油的摩尔质量Ml=0.09kg/mol.若把油膜看成单分子层,每个油分子看成球形,那么:
(a)油分子的直径为多大?
(b)由以上数据可测出的阿伏加德罗常数大约为多少?(保留一位有效数字)
分析:(1)一定质量的理想气体发生等容变化时,压强P与温度T的成正比,即
=C(常量).
(2)缓慢推拉活塞,气体温度不变,根据玻意耳定律,当压缩气体时,体积减小,则压强增大.由于温度不变,不论体积增大还是减小,理想气体的内能都不变.
(3)(a)根据油膜法测出分子直径的原理d=
,代入数据计算即可.
(b)每个分子看成球形,则每个分子的体积V=
πd3=
?(
)3,则1mol这种油的体积Vl=
=NA?V=NA?
π(
)3,化简并代入数据计算,可得阿伏加德罗常数NA的值.
| P |
| T |
(2)缓慢推拉活塞,气体温度不变,根据玻意耳定律,当压缩气体时,体积减小,则压强增大.由于温度不变,不论体积增大还是减小,理想气体的内能都不变.
(3)(a)根据油膜法测出分子直径的原理d=
| V |
| S |
(b)每个分子看成球形,则每个分子的体积V=
| 1 |
| 6 |
| π |
| 6 |
| V |
| S |
| Ml |
| ρ |
| 1 |
| 6 |
| V |
| S |
解答:解:(1)一定质量的理想气体发生等容变化,压强P与温度T的成正比.故选C.
(2)该同学往里缓慢地推和拉活塞,理想气体温度不变,是等温变化.当压缩气体时,体积减小,则压强增大.由于温度不变,不论体积增大还是减小,气体内能都不变.
(3)(a)利用油膜法测出分子直径
d=
=
m=7.1×10-10m
(b)每个分子看成球形,则每个分子的体积V=
πd3=
?(
)3
1mol这种油的体积Vl=
=NA?V=NA?
π(
)3
所以NA=
=
mol-1=6×1023mol-1
故答案为:(1)C,(2)增大,0.
(3)(a)油分子的直径为7.1×10-10m.(b)阿伏加德罗常数大约为6×1023mol-1.
(2)该同学往里缓慢地推和拉活塞,理想气体温度不变,是等温变化.当压缩气体时,体积减小,则压强增大.由于温度不变,不论体积增大还是减小,气体内能都不变.
(3)(a)利用油膜法测出分子直径
d=
| V |
| S |
| 0.5×10-3×10-6 |
| 0.7 |
(b)每个分子看成球形,则每个分子的体积V=
| 1 |
| 6 |
| π |
| 6 |
| V |
| S |
1mol这种油的体积Vl=
| Ml |
| ρ |
| 1 |
| 6 |
| V |
| S |
所以NA=
| 6Ml | ||
πρ?(
|
| 6×9×10-2 |
| 3.14×0.8×103×(7.1×10-10)3 |
故答案为:(1)C,(2)增大,0.
(3)(a)油分子的直径为7.1×10-10m.(b)阿伏加德罗常数大约为6×1023mol-1.
点评:根据油膜法测分子直径的原理可求出油分子的直径,根据油的摩尔质量和密度算出其摩尔体积,然后求出每个油分子的体积,即可正确解答本题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 A.(选修模块3-3)
A.(选修模块3-3)
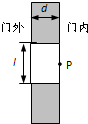
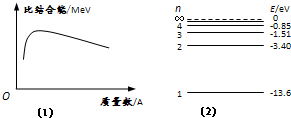 A.小质量数的原子核质量亏损最大
A.小质量数的原子核质量亏损最大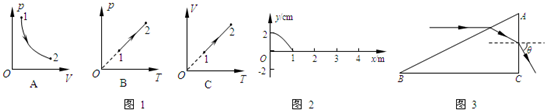
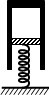 ,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将