长为a.b宽为的矩形线框有n匝.每匝线圈电阻为R.如图所示.对称轴MN的左侧处在磁感应强度为B的匀强磁场中.第一次将线框从磁场中以速度v匀速拉出,第二次让线框以ω=2v/b的角速度转过90°角．那么( )A．通过导线横截面的电量q1:q2=1:nB．通过导线横截面的电量q1:q2=1:1C．线框发热功率P1:P2=2n:1D．线框发热功率P1:P2=2:1 题目和参考答案——青夏教育精英家教网—

题目内容

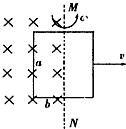长为a、b宽为的矩形线框有n匝，每匝线圈电阻为R，如图所示，对称轴MN的左侧处在磁感应强度为B的匀强磁场中，第一次将线框从磁场中以速度v匀速拉出；第二次让线框以ω=2v/b的角速度转过90°角．那么（　　）

A．通过导线横截面的电量q₁：q₂=1：n

B．通过导线横截面的电量q₁：q₂=1：1

C．线框发热功率P₁：P₂=2n：1

D．线框发热功率P₁：P₂=2：1

分析：根据法拉第电磁感应定律，得出感应电动势E=n

△?

△t

，结合闭合电路欧姆定律I=

与电量表达式Q=It，即可解得电量q=

△?

，从而即可求解．
平均感应电动势E=n

△?

△t

，瞬时感应电动势E=BLv．分别求出感应电流的大小，再根据热功率的表达式P=I²nR，进行比较．

解答：解：A、根据法拉第电磁感应定律，得出感应电动势E=n

△?

△t

，结合闭合电路欧姆定律I=

与电量表达式Q=It，即可解得电量q=

△?

，虽然两次的运动方式不同，但它们的磁通量的变化量相同，因此它们的电量之比为1：1，故A错误，B正确；
C、由平均感应电动势E=n

△?

△t

，瞬时感应电动势E=BLv．则感应电流的大小之比即为感应电动势大小之比，则为Bav：

2ω

：1
再根据线框的发热功率P=I²nR，可知，线框发热功率P₁：P₂=2：1，故C错误，D正确；
故选BD

点评：解决本题的关键掌握法拉第电磁感应定律、闭合电路欧姆定律与电量表达式相综合而得q=

△?

，同时理解发热功率与什么因素有关，并对于这些基础知识，要加强理解和应用，平时练习不可忽视．

练习册系列答案

相关题目

如图，长为a、宽为b的矩形线框的左半侧处在磁感应强度为B的匀强磁场中，磁场方向与线框平面垂直，线框的对称轴MN恰与磁场边缘平齐．若第一次将线框从磁场中以恒定速度v向右匀速拉出，第二次以同样大小的线速度v让线框转过90？．两次过程中，线框产生的平均感应电动势之比为

；第一次线框运动到磁场边缘时与第二次线框转过90？时（左侧边均未离开磁场），两次线框的瞬时发热功率之比为

1：1

．

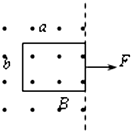如图所示，长为a、宽为b的矩形线圈，电阻为r，处在磁感应强度为B的匀强磁场边缘，磁场方向垂直于纸面向外，线圈与磁感线垂直．用力F将线圈向右以速度v匀速拉出磁场的过程中（　　）

（18分）

（1）如图所示，abcd为单匝矩形线圈，边长ab＝10cm，bc＝20cm。该线圈的一半位于具有理想边界、磁感应强度为0.1T、宽为20cm的匀强磁场中，磁场方向与线圈平面垂直。若线圈绕通过ab边的轴以100p rad/s的角速度匀速旋转，当线圈由图示位置转过90°时的瞬时感应电动势大小为___________V。

（2）某同学利用如图甲所示的实验装置验证机械能守恒定律．

（I）请指出该同学在实验操作中存在的两处明显错误或不当：

① ；

② 。

（II）该同学经正确操作得到如图乙所示的纸带，取连续的六个点A、B、C、D、E、F为计数点，测得点A到B、C、D、E、F的距离分别为h₁、h₂、h₃、h₄、h₅，若打点的时间间隔为T，则打E点时重物速度的表达式为v_E=

（3）冬、春季节降水量少，广东沿海附近水位较低，涨潮时海水倒灌出现所谓咸潮现象，使沿海地区的城市自来水中的离子浓度较高，水质受到影响，为了研究咸潮出现的规律，某同学设计了一个监测河水电阻率的实验。它在一根均匀的长玻璃管两端装上两个橡胶塞和铂电极，如下图(1)所示，两电极相距L=0.314m，其间充满待测的河水。安装前他用如下图(2)的游标卡尺（图为卡尺的背面）测量玻璃管的内径，结果如下图(3)所示。

他还选用了以下仪器：量程15V、内阻300kΩ的电压表，量程300μA、内阻50Ω的电

流表，最大阻值为1kΩ的滑动变阻器，电动势E=12V、内阻r=6Ω的电池组，开关等各一个，以及导线若干。下图(4)坐标中包括坐标为（0，0）的点在内的9个点表示他测得的9组电流I、电压U的值。

根据以上材料完成以下问题：

（a）测量玻璃管内径时，应将上图(2)中的游标卡尺的A、B、C三部分中的__________________与玻璃管内壁接触（填代号）；

（b）玻璃管的内径d=___________mm；

（c）图(4)中的9个点表示实验中测得的9组电流I、电压U的值，试写出根据此图求R值的步骤：

（d）上图(5)中的实物仪器部分已连线，将其他部分连接成能测出上图(4)数据的实物连接图；

（e）开头闭合前滑动变阻器的滑片应先滑至___________端。

（18分）
（1）如图所示，abcd为单匝矩形线圈，边长ab＝10cm，bc＝20cm。该线圈的一半位于具有理想边界、磁感应强度为0.1T、宽为20cm的匀强磁场中，磁场方向与线圈平面垂直。若线圈绕通过ab边的轴以100p rad/s的角速度匀速旋转，当线圈由图示位置转过90°时的瞬时感应电动势大小为___________V。

（2）某同学利用如图甲所示的实验装置验证机械能守恒定律．
（I）请指出该同学在实验操作中存在的两处明显错误或不当：
①                                             ；
②                                             。
（II）该同学经正确操作得到如图乙所示的纸带，取连续的六个点A、B、C、D、E、F为计数点，测得点A到B、C、D、E、F的距离分别为h₁、h₂、h₃、h₄、h₅，若打点的时间间隔为T，则打E点时重物速度的表达式为v_E=

（3）冬、春季节降水量少，广东沿海附近水位较低，涨潮时海水倒灌出现所谓咸潮现象，使沿海地区的城市自来水中的离子浓度较高，水质受到影响，为了研究咸潮出现的规律，某同学设计了一个监测河水电阻率的实验。它在一根均匀的长玻璃管两端装上两个橡胶塞和铂电极，如下图(1)所示，两电极相距L=0.314m，其间充满待测的河水。安装前他用如下图(2)的游标卡尺（图为卡尺的背面）测量玻璃管的内径，结果如下图(3)所示。
他还选用了以下仪器：量程15V、内阻300kΩ的电压表，量程300μA、内阻50Ω的电
流表，最大阻值为1kΩ的滑动变阻器，电动势E=12V、内阻r=6Ω的电池组，开关等各一个，以及导线若干。下图(4)坐标中包括坐标为（0，0）的点在内的9个点表示他测得的9组电流I、电压U的值。

根据以上材料完成以下问题：
（a）测量玻璃管内径时，应将上图(2)中的游标卡尺的A、B、C三部分中的__________________与玻璃管内壁接触（填代号）；
（b）玻璃管的内径d=___________mm；
（c）图(4)中的9个点表示实验中测得的9组电流I、电压U的值，试写出根据此图求R值的步骤：


（d）上图(5)中的实物仪器部分已连线，将其他部分连接成能测出上图(4)数据的实物连接图；
（e）开头闭合前滑动变阻器的滑片应先滑至___________端。

试题分类