题目内容
18.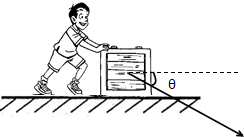 如图所示,质量m=30kg的箱子静止于地面上,箱子与地面间的动摩擦因数μ=0.5.现一同学用大小为360N,方向与水平方向成θ=37°斜向下的恒定推力F使木箱在地面上做匀加速直线运动,3s末撤去该力,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,质量m=30kg的箱子静止于地面上,箱子与地面间的动摩擦因数μ=0.5.现一同学用大小为360N,方向与水平方向成θ=37°斜向下的恒定推力F使木箱在地面上做匀加速直线运动,3s末撤去该力,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)撤去推力时,木箱的速度大小;
(2)撤去推力后,木块继续滑行的距离.
分析 (1)根据牛顿第二定律求出在推力作用下的加速度,结合速度时间公式求出木箱的速度.
(2)根据牛顿第二定律求出撤去推力后的加速度,结合速度位移公式求出木块继续滑行的距离.
解答 解:(1)根据牛顿第二定律得,木箱的加速度${a}_{1}=\frac{Fcos37°-μ(mg+Fsin37°)}{m}$=$\frac{360×0.8-0.5×(300+360×0.6)}{30}$m/s2=1m/s2.
撤去推力后木箱的速度v=a1t1=1×3m/s=3m/s.
(2)撤去推力后,木箱的加速度大小${a}_{2}=\frac{μmg}{m}=μg=5m/{s}^{2}$,
根据速度位移公式得,木块继续滑行的距离$x=\frac{{v}^{2}}{2{a}_{2}}=\frac{9}{10}m=0.9m$.
答:(1)撤去推力时,木箱的速度大小为3m/s;
(2)撤去推力后,木块继续滑行的距离为0.9m.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,难度不大.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
9.关于环绕地球做圆周运动的人造卫星,下列说法正确的是( )
| A. | 在同一轨道上运动的不同形状、不同质量的卫星线速度大小也不同 | |
| B. | 卫星绕地球做圆周运动时,其线速度一定不会大于第一宇宙速度 | |
| C. | 为通信需要,可以发射一颗“定位”于南阳市正上方的同步卫星 | |
| D. | 可以发射一颗卫星,使其运动的轨道平面始终与地球上某一经线平面相重合 |
13.河水的流速随离河岸一侧的距离的变化关系如图甲所示,船在静水中的速度与时间的关系如图乙所示,若要使船以最短时间渡河,则( )
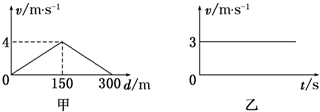

| A. | 船在行驶过程中,船头始终与河岸垂直 | |
| B. | 船在行驶过程中,船头方向要随着水的流速变化而不断调整 | |
| C. | 船渡河的最短时间是60s | |
| D. | 船在河水中航行的轨迹是一条直线 |
10.用多用电表欧姆挡测电阻时,下列说法中错误的是( )
| A. | 测量前必须调零,而且每测一次电阻都要重新调零 | |
| B. | 测量电阻时,用两手碰表笔的金属杆,其测量值偏小 | |
| C. | 用多用表测60W灯泡的电阻,其阻值比用额定电压和额定功率算出的电阻值小 | |
| D. | 使用完毕应当拔出表笔,并把选择开关旋到OFF挡或交流电压最高挡 |
5. 在60周年国庆盛典上,游行的队伍和彩车依次从天安门前经过(如图),以北京长安街为坐标轴x,向西为正方向,以天安门中心所对的长安街中心为坐标原点O,建立一维坐标系,一辆彩车最初在原点以东3km处,一段时间后行驶到原点以西2km处.这辆彩车最初位置和最终位置分别是( )
在60周年国庆盛典上,游行的队伍和彩车依次从天安门前经过(如图),以北京长安街为坐标轴x,向西为正方向,以天安门中心所对的长安街中心为坐标原点O,建立一维坐标系,一辆彩车最初在原点以东3km处,一段时间后行驶到原点以西2km处.这辆彩车最初位置和最终位置分别是( )
 在60周年国庆盛典上,游行的队伍和彩车依次从天安门前经过(如图),以北京长安街为坐标轴x,向西为正方向,以天安门中心所对的长安街中心为坐标原点O,建立一维坐标系,一辆彩车最初在原点以东3km处,一段时间后行驶到原点以西2km处.这辆彩车最初位置和最终位置分别是( )
在60周年国庆盛典上,游行的队伍和彩车依次从天安门前经过(如图),以北京长安街为坐标轴x,向西为正方向,以天安门中心所对的长安街中心为坐标原点O,建立一维坐标系,一辆彩车最初在原点以东3km处,一段时间后行驶到原点以西2km处.这辆彩车最初位置和最终位置分别是( )| A. | 3km 2km | B. | -3km 2km | C. | 3km-2km | D. | -3km-2km |
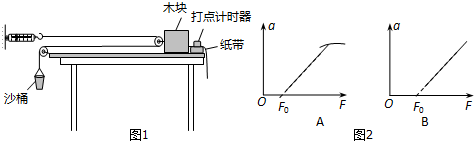


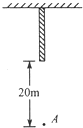 如图一条绳子一端悬挂于某点后,让其放开自由下落,若全条绳子经过悬挂绳子下方20m处的A点的时间是1s,则该绳子长应为多少(g取10m/s2)
如图一条绳子一端悬挂于某点后,让其放开自由下落,若全条绳子经过悬挂绳子下方20m处的A点的时间是1s,则该绳子长应为多少(g取10m/s2)