题目内容
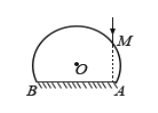
【题目】如图,玻璃球冠的折射率为![]() ,其底面镀银,底面的半径是球半径的
,其底面镀银,底面的半径是球半径的![]() 倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点.求该光线从球面射出的方向相对于其初始入射方向的偏角.
倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点.求该光线从球面射出的方向相对于其初始入射方向的偏角.
【答案】150°
【解析】
设球半径为R,球冠地面中心为O′,连接OO′,则OO′⊥AB
令∠OAO′=α
则: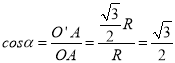 …①
…①
即∠OAO′=α=30°…②
已知MA⊥AB,所以∠OAM=60°…③
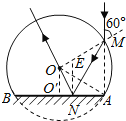
设图中N点为光线在球冠内地面上的反射点,光路图如图所示.
设光线在M点的入射角为i,折射角为r,在N点的入射角为i′,反射角为i″,玻璃的折射率为n.
由于△OAM为等边三角形,所以入射角i=60°…④
由折射定律得:sini=nsinr…⑤
代入数据得:r=30°…⑥
作N点的法线NE,由于NE∥MA,所以i′=30°…⑦
由反射定律得:i″=30°…⑧
连接ON,由几何关系可知△MAN≌△MON,则∠MNO=60°…⑨
由⑦⑨式可得∠ENO=30°
所以∠ENO为反射角,ON为反射光线.由于这一反射光线垂直球面,所以经球面再次折射后不改变方向.所以,该光线从球面射出的方向相对于其初始入射方向的偏角为β=180°-∠ENO=150°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目