题目内容
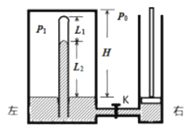
【题目】如图所示,两个导热的圆筒底部有一条细短管连通,圆筒内装有约20cm深的水银,K为阀门,处于关闭状态。左侧大圆筒的横截面积![]() ,水银面到圆筒顶部的高度
,水银面到圆筒顶部的高度![]() ,水银上方是空气,空气的压强
,水银上方是空气,空气的压强![]() ,室温
,室温![]() 。左侧圆筒中竖直放置一根托里拆利管,管的横截面积远小于两圆筒的横截面积,托里拆利管中水银上方有氮气,氮气柱的长度
。左侧圆筒中竖直放置一根托里拆利管,管的横截面积远小于两圆筒的横截面积,托里拆利管中水银上方有氮气,氮气柱的长度![]() ,水银柱的高度
,水银柱的高度![]() 。右侧小圆筒的横截面积
。右侧小圆筒的横截面积![]() ,一个活塞紧贴水银放置。已知大气压强
,一个活塞紧贴水银放置。已知大气压强![]() 。求:
。求:
(Ⅰ)若环境温度缓慢升高![]() ,左侧圆筒内空气的压强变为多大?
,左侧圆筒内空气的压强变为多大?
(Ⅱ)在环境温度为![]() 时,用力控制右侧圆筒中活塞,打开阀门K,使活塞缓慢升高
时,用力控制右侧圆筒中活塞,打开阀门K,使活塞缓慢升高![]() 后固定,则托里拆利管中氮气柱的长度最终变为多大?(结果可以带跟号)
后固定,则托里拆利管中氮气柱的长度最终变为多大?(结果可以带跟号)
【答案】(Ⅰ)![]() ,(Ⅱ)
,(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)环境温度缓慢升高60℃的过程为等容变化过程,运用查理定律即可求出末态左侧圆筒内空气的压强;(Ⅱ)环境温度不变,左侧空气发生等温变化,对其运用玻意耳定律即可求出升温后空气的压强,利用平衡求出托里拆利管中封闭氮气的压强,再对氮气运用理想气体的状态方程即可求出托里拆利管中氮气柱的终变长度.
(Ⅰ)设升温后左侧大圆筒空气的压强变为![]() ,因阀门关闭,大圆筒内空气做等容变化,有:
,因阀门关闭,大圆筒内空气做等容变化,有: ![]() ,其中:
,其中: ![]() ,
, ![]()
代入数值解得: ![]()
(Ⅱ)阀门打开并控制活塞缓慢上升![]() 时,因左侧大圆筒中空气的压强大于外界大气压强,左侧大圆筒水平面下降高度设为
时,因左侧大圆筒中空气的压强大于外界大气压强,左侧大圆筒水平面下降高度设为![]() ,根据体积不变原理,则有:
,根据体积不变原理,则有: ![]()
解得: ![]() =5cm
=5cm
同时,左侧大圆筒中的空气做等温变化,设空气高度变为![]() ,空气的压强变为
,空气的压强变为![]() ,则有:
,则有: ![]()
代入数值解得: ![]()
设托里拆利管中密封氮气柱的横截面积为S,最终长度为![]() ,其初始压强为
,其初始压强为![]() ,最终压强为
,最终压强为![]() ,根据理想气体状态方程,有:
,根据理想气体状态方程,有: ![]()
其中: ![]() ,
,
![]()
解得氮气柱的最终长度为: ![]()

练习册系列答案
相关题目