题目内容
20.地球绕太阳运动的周期与月球绕地球运动周期的比值为P,它们的轨道半径之比为q′若它们的运动都可以看作是匀速圆周运动,则太阳质量与地球质量之经为( )| A. | $\frac{{q}^{3}}{{p}^{2}}$ | B. | p2•q3 | C. | $\frac{{p}^{3}}{{q}^{2}}$ | D. | p3•q2 |
分析 地球绕太阳做圆周运动、月球绕地球做圆周运动,万有引力提供向心力,应用牛顿第二定律求出地球与太阳的质量,然后求出质量之比.
解答 解:万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{{r}^{2}}$=m$({\frac{2π}{T})}^{2}$r,解得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,
$\frac{{M}_{太}}{{M}_{地}}$=$\frac{\frac{4{π}^{2}{r}_{地}^{3}}{G{T}_{地}^{2}}}{\frac{4{π}^{2}{r}_{月}^{3}}{G{T}_{月}^{2}}}$=$\frac{{r}_{地}^{3}{T}_{月}^{2}}{{r}_{月}^{3}{T}_{地}^{2}}$=$\frac{{q}^{3}}{{p}^{2}}$,故A正确;
故选:A.
点评 本题考查了求太阳质量与地球质量之比,应用万有引力公式与牛顿第二定律求出地球与太阳的质量,然后再求出太阳与地球质量之比,要掌握比值法的应用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
10. 如图所示,在一条倾斜的、静止不动的传送带上,有一个滑块能够自由地向下滑动,该滑块由上端自由地滑到底端所用时间为t1,如果传送带向上以速度v0运动起来,保持其它条件不变,该滑块由上端滑到底端所用的时间为t2,那么( )
如图所示,在一条倾斜的、静止不动的传送带上,有一个滑块能够自由地向下滑动,该滑块由上端自由地滑到底端所用时间为t1,如果传送带向上以速度v0运动起来,保持其它条件不变,该滑块由上端滑到底端所用的时间为t2,那么( )
 如图所示,在一条倾斜的、静止不动的传送带上,有一个滑块能够自由地向下滑动,该滑块由上端自由地滑到底端所用时间为t1,如果传送带向上以速度v0运动起来,保持其它条件不变,该滑块由上端滑到底端所用的时间为t2,那么( )
如图所示,在一条倾斜的、静止不动的传送带上,有一个滑块能够自由地向下滑动,该滑块由上端自由地滑到底端所用时间为t1,如果传送带向上以速度v0运动起来,保持其它条件不变,该滑块由上端滑到底端所用的时间为t2,那么( )| A. | t1=t2 | B. | t1>t2 | C. | t1<t2 | D. | 不能确定 |
8. 如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )
如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )
 如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )
如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )| A. | mAsinα=mBsinβ | B. | mAsinβ=mBsinα | C. | mAcosα=mBcosβ | D. | mAcosβ=mBcosα |
15. 为了节省能量,某商场安装了智能化的电动扶梯.无人乘坐时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速转动.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则下列说法正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘坐时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速转动.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则下列说法正确的是( )
 为了节省能量,某商场安装了智能化的电动扶梯.无人乘坐时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速转动.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则下列说法正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘坐时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速转动.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示,则下列说法正确的是( )| A. | 顾客始终受到三个力的作用 | |
| B. | 顾客始终处于超重状态 | |
| C. | 扶梯对顾客作用力的方向先指向左上方,再竖直向上 | |
| D. | 扶梯对顾客作用力的方向先指向右上方,再竖直向上 |
12. 一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )
一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )
 一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )
一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )| A. | $\frac{{{v}_{0}}^{2}}{2g}$ | B. | $\frac{{{v}_{0}}^{2}}{2gsinθ}$ | C. | $\frac{{{v}_{0}}^{2}}{4gsinθ}$ | D. | $\frac{{{v}_{0}}^{2}}{2gcosθ}$ |
9.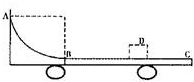 如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )
如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )
 如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )
如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )| A. | 其他量不变,R越大s越大 | B. | 其他量不变,μ越大s越大 | ||
| C. | 其他量不变,m越大s越大 | D. | 其他量不变,M越大s越大 |
 在用打点计时器“验证机械能守恒定律”的实验中,质量m=1.0kg的重物拖着纸带竖直下落,打点计时器在纸带上打下一系列的点,如图所示,相邻计数点时间间隔为0.04s,当地重力加速度g=9.8m/s2.P为纸带运动的起点,从打下P点到打下B点的过程中重物重力势能的减小量△Ep=2.28J,在此过程中重物动能的增加量△Ek=2.26J(结果保留三位有效数字).
在用打点计时器“验证机械能守恒定律”的实验中,质量m=1.0kg的重物拖着纸带竖直下落,打点计时器在纸带上打下一系列的点,如图所示,相邻计数点时间间隔为0.04s,当地重力加速度g=9.8m/s2.P为纸带运动的起点,从打下P点到打下B点的过程中重物重力势能的减小量△Ep=2.28J,在此过程中重物动能的增加量△Ek=2.26J(结果保留三位有效数字). 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,引力常量为G,自转周期为T,求:
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,引力常量为G,自转周期为T,求: