题目内容
【题目】“神舟”六号飞船完成了预定空间科学和技术试验任务后，返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回，在离地10km的高度打开阻力降落伞减速下降，这一过程中若返回舱所受阻力与速度的平方成正比，比例系数（空气阻力系数）为k，设返回舱总质量M=3000kg，所受空气浮力恒定不变，且认为竖直降落。从某时刻开始计时，返回舱的运动v-t图象如图中的AD曲线所示，图中AB是曲线在A点的切线，切线交于横轴一点B的坐标为（8，0），CD是平行横轴的直线，交纵轴于C点C的坐标为（0，8）。g取10m/s2，请解决下列问题：
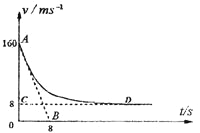
（1）在初始时刻v0=160m/s时，它的加速度多大？
（2）推证空气阻力系数k的表达式并算出其数值。
（3）返回舱在距离高度h=1m时，飞船底部的4个反推力小火箭点火工作，使其速度由8m/s迅速减至1m/s后落在地面上，若忽略燃料质量的减少对返回舱总质量的影响，并忽略此阶段速度变化而引起空气阻力的变化，试估算每支小火箭的平均推力（计算结果取两位有效数字）
【答案】（1）20m/s2（2）
； 2.35kg/m（3）2.4×104N
【解析】试题分析：过A点切线的斜率为初始时刻的加速度；根据牛顿第二定律，列出当速度为160m/s时的牛顿第二定律表达式和当速度为8m/s时匀速运动的表达式，联立两方程组解出k；在距地高度h=1m前，返回舱已处于匀速运动状态，返回舱所受浮力、阻力与重力的合力为零．减速运动的加速度由火箭推力产生，根据匀减速运动求出加速度，再根据牛顿第二定律求出每支小火箭的平均推力。
（1）根据速度图象性质可知，在初始v0=160m/s时，过A点切线的斜率既为此时的加速度，设为a1，其大小为： 
（2）由图知，返回舱的v – t图的斜率逐渐减小，最后是以v1=8m/s的速度作匀速运动。设返回舱所受空气浮力为f，在t=0时， 根据牛顿第二定律则有：
速度为v1=8m/s时，返回舱受力平衡，即有： 
由以上并代入数据解得： 
（3）设每支小火箭的平均推力为F0，反推加速度大小为a2，着地速度为v2
由题意知，返回舱在距离地高度h=1m前，已处于匀速运动状态。故返回舱在着地前的加速度由4个小火箭的反推力产生根据牛顿第二定律： 
又由运动学公式知： 
联立以上并代入数据解得：
