题目内容
11. 如图所示,坡道顶端距水平面高度为h,质量为m1的小物块A从摩擦可以忽略的坡道顶端由静止滑下,进入光滑水平面上的滑道时无机械能损失,为使A制动,将轻弹簧的一端固定在水平滑道延长线M处的墙上,另一端与质量为m2的挡板B相连,弹簧处于原长时,B恰好位于滑道的末端O点,A与B碰撞时间极短,碰撞后粘合在一起共同压缩弹簧至最短后被锁定,重力加速度为g,那么( )
如图所示,坡道顶端距水平面高度为h,质量为m1的小物块A从摩擦可以忽略的坡道顶端由静止滑下,进入光滑水平面上的滑道时无机械能损失,为使A制动,将轻弹簧的一端固定在水平滑道延长线M处的墙上,另一端与质量为m2的挡板B相连,弹簧处于原长时,B恰好位于滑道的末端O点,A与B碰撞时间极短,碰撞后粘合在一起共同压缩弹簧至最短后被锁定,重力加速度为g,那么( )| A. | 运动过程中A和B组成的系统机械能守恒 | |
| B. | 运动过程中A和B组成的系统动量守恒 | |
| C. | A物体与B碰撞前的速度大小为$\sqrt{gh}$ | |
| D. | A物体与B碰撞后的速度大小为$\frac{m_1}{{{m_1}+{m_2}}}\sqrt{2gh}$ |
分析 两个物块碰撞后粘在一起,机械能不守恒;二者在碰撞的过程中,水平方向的动量守恒;物块A在坡道上下滑时,只有重力做功,机械能守恒,根据机械能守恒定律求出物块A在与挡板B碰撞前的瞬间速度v的大小.根据动量守恒定律即可求出碰撞后的速度.
解答 解:A、两个物块碰撞后粘在一起,属于完全非弹性碰撞,机械能不守恒;故A错误;
B、A与B在碰撞的过程中,由于时间短,弹簧没有来得及发生形变,所以在水平方向、竖直方向二者受到的合外力都是0,系统的动量守恒,但在A与B一起压缩弹簧的过程中,A与B受到的弹簧的弹力不能忽略不计,所以整个的过程中二者的动量不守恒.故B错误;
C、A到O的过程中,由机械能守恒定律得:${m}_{1}gh=\frac{1}{2}{m}_{1}{v}^{2}$
解得:v=$\sqrt{2gh}$.
故物块A在与挡板B碰撞前的瞬间速度v的大小为$\sqrt{2gh}$.故C错误;
D、A、B在碰撞过程中内力远大于外力,选取向左为正方向,由动量守恒,得:m1v=(m1+m2)v′
所以:$v′=\frac{{m}_{1}}{{m}_{1}+{m}_{2}}v=\frac{{m}_{1}\sqrt{2gh}}{{m}_{1}+{m}_{2}}$.故D正确;
故选:D
点评 本题考查了动量和能量问题,有一定的难度,关键运用能量守恒时,找出有哪些能量发生了转化.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
10.一石块从楼顶自由落下.不计空气阻力,取 g=10m/s2.在石块下落的过程中( )
| A. | 第 1 s 内下落的高度为 1 m | B. | 第 1 s 内下落的高度为 5 m | ||
| C. | 第 1 s 内下落的高度为 10 m | D. | 第 1 s 内下落的高度为 15 m |
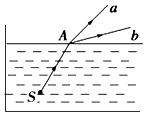
2.如图所示,水下光源S向水面A点发射一束光线,折射光线分别为a、b两束.则( )

| A. | a光的频率小于b光的频率 | |
| B. | 在真空中a光的速度大于b光的速度 | |
| C. | 若a光为绿光,则b可能为紫光 | |
| D. | 若保持入射点A位置不变,将入射光线瞬时针旋转,从水面上方观察,a光先消失 | |
| E. | 用同一双缝干涉实验装置分别用a、b光做实验,a光干涉相邻条纹间距大于b光干涉相邻条纹间距 |
16.物体静止在光滑水平面上.从某一时刻起用水平恒力F推物体,则在该力刚开始作用的瞬间( )
| A. | 立即产生加速度,但速度仍然为零 | B. | 立即产生速度,但加速度仍然为零 | ||
| C. | 立即同时产生加速度和速度 | D. | 速度和加速度均为零 |
3.关于物体的惯性,下列说法中正确的是( )
| A. | 物体保持匀速直线运动状态或静止时才有惯性 | |
| B. | 物体在不受力或所受外力的合力为零时才有惯性 | |
| C. | 改变一个物体的惯性,必须要有力的作用 | |
| D. | 一切物体都有惯性,与物体的运动状态无关 |
20.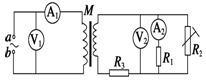 如图所示,M是一小型理想变压器,接线柱a、b接在正弦交流电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,其阻值随温度升高而减小.电流表
如图所示,M是一小型理想变压器,接线柱a、b接在正弦交流电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,其阻值随温度升高而减小.电流表 为值班室的显示器,显示通过R1的电流,电压表
为值班室的显示器,显示通过R1的电流,电压表 显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
 如图所示,M是一小型理想变压器,接线柱a、b接在正弦交流电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,其阻值随温度升高而减小.电流表
如图所示,M是一小型理想变压器,接线柱a、b接在正弦交流电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,其阻值随温度升高而减小.电流表 为值班室的显示器,显示通过R1的电流,电压表
为值班室的显示器,显示通过R1的电流,电压表 显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )| A. |  的示数不变, 的示数不变, 的示数增大 的示数增大 | B. |  的示数减小, 的示数减小, 的示数增大 的示数增大 | ||
| C. |  的示数不变, 的示数不变, 的示数增大 的示数增大 | D. |  的示数不变, 的示数不变, 的示数减小 的示数减小 |
1.关于功率公式 P=$\frac{W}{t}$ 和 P=Fv 的说法正确的是( )
| A. | 由 P=$\frac{W}{t}$ 只能求某一时刻的瞬时功率 | |
| B. | 从 P=Fv 知,汽车的功率与它的速度成正比 | |
| C. | 由 P=Fv 只能求某一时刻的瞬时功率 | |
| D. | 从 P=Fv 知,当汽车发动机功率一定时,牵引力与速度成反比 |
