题目内容
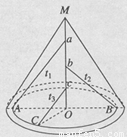
如图所示,在圆锥形内部有三根固定的光滑细杆, A、B、C为圆锥底部同一圆周上的三个点,三杆Aa、bB、cC与水平底面的夹角分别为60o、45o、30o。每根杆上都套着一个小滑环(图中未画出),三个滑环分别从a、b、c处由静止释放(忽略阻力),用tl、t2、t3依次表示各滑环到达A、B、C所用的时间,则
A.tl>t2>t3 B.t1 <t2< t3 C.tl=t3<t2 D.t1=t3> t2
【答案】
D
【解析】
试题分析:由牛顿第二定律可知滑环在杆上做初速度为0,加速度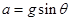 的匀加速直线运动,假设A、B、C三点所在圆的半径为
的匀加速直线运动,假设A、B、C三点所在圆的半径为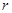 ,则
,则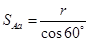 =2
=2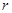 ,
,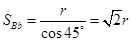 ,
,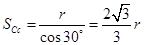 ,又根据匀变速直线运动公式
,又根据匀变速直线运动公式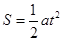 得
得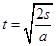 ,代入数据可知D正确,A、B、C错误。
,代入数据可知D正确,A、B、C错误。
考点:本题考查牛顿第二定律与匀变速直线运动的综合应用。

练习册系列答案
相关题目
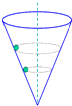 如图所示,在光滑的圆锥形漏斗内壁,小球紧贴着漏斗在水平面内做匀速圆周运动,关于小球的受力情况,下列说法正确的是( )
如图所示,在光滑的圆锥形漏斗内壁,小球紧贴着漏斗在水平面内做匀速圆周运动,关于小球的受力情况,下列说法正确的是( )| A、受重力、支持力、向心力 | B、受重力、支持力 | C、只受重力 | D、只受支持力 |
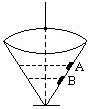 如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁,在不同的水平面上做匀速圆周运动.则以下叙述正确的是( )
如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁,在不同的水平面上做匀速圆周运动.则以下叙述正确的是( ) 如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁,在不同的水平面上做匀速圆周运动.则以下叙述正确的是( )
如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小物块A和B,它们分别紧贴漏斗的内壁,在不同的水平面上做匀速圆周运动.则以下叙述正确的是( )