题目内容
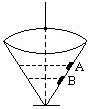如图所示，在固定的圆锥形漏斗的光滑内壁上，有两个质量相等的小物块A和B，它们分别紧贴漏斗的内壁，在不同的水平面上做匀速圆周运动．则以下叙述正确的是（ ）分析：两球在不同的水平面上做半径不同的匀速圆周运动，因为所受的重力与支持力分别相等，即向心力相同，由牛顿第二定律可以解得其线速度间、角速度间、周期间的关系．
解答：解：
对A、B两球进行受力分析，两球均只受重力和漏斗给的支持力FN．如图所示．
设内壁与水平面的夹角为θ．
根据牛顿第二定律有：mgtanθ=m
则v=
，半径大的线速度大，所以A的线速度大于B的线速度．
ω=
=
，知半径越大，角速度越小，所以A的角速度小于B的角速度．
T=
，则角速度越大，周期越小，所以A的周期大于B的周期．
支持力FN=
，知物块A对漏斗内壁的压力等于物块B对漏斗内壁的压力．
故AD正确，B、C错误．
故选AD．
对A、B两球进行受力分析，两球均只受重力和漏斗给的支持力FN．如图所示．设内壁与水平面的夹角为θ．
根据牛顿第二定律有：mgtanθ=m
| v2 |
| r |
则v=
| grtanθ |
ω=
| v |
| r |
|
T=
| 2π |
| ω |
支持力FN=
| mg |
| cosθ |
故AD正确，B、C错误．
故选AD．
点评：对物体进行受力分析，找出其中的相同的量，再利用圆周运动中各物理量的关系式分析比较，能较好的考查学生这部分的基础知识的掌握情况．
练习册系列答案
相关题目
如图所示，在光滑的水平面上停放着一辆平板车，在车上的左端放有一木块B．车左边紧邻一个固定在竖直面内、半径为R的
如图所示，原来静止的圆环形线圈通有逆时针方向的电流I，在其直径AB上靠近B点放置一根垂直于线圈平面的固定不动的长直导线，并通以电流I，方向垂直纸面向外，此时环形线圈的运动情况是（ ）
（2013?商丘三模）如图所示，在固定的光滑水平杆（杆足够长）上，套有一个质量为m=0.5kg的光滑金属圆环，轻绳一端拴在环上，另一端系着一个质量为M=1.98kg的木块，现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中（不计空气阻力和子弹与木块作用的时间，g取10m/s2），求：
