题目内容
倾角θ为37°的斜面与水平面如图平滑相接，A、B两完全相同的物块静置于斜面上相距
，B距斜面底端的P点的距离
，物块与斜面及水平面的动摩擦因数均为
．现由静止释放物块A后1秒钟再释放物块B．设AB碰撞的时间极短，碰后就粘连在一起运动．试求：
，B距斜面底端的P点的距离，物块与斜面及水平面的动摩擦因数均为．现由静止释放物块A后1秒钟再释放物块B．设AB碰撞的时间极短，碰后就粘连在一起运动．试求：（1）B物块释放后多长时间，AB两物块发生碰撞？
（2）AB最后停在距斜面底端P点多远处？取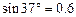
，
，
．
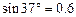，，．（1）
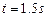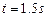（2）
（2）（1）设B物体的质量为m，加速下滑时的加速度为a，其在斜面上时的受力情况如图所示。由牛顿第二定律得：
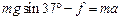
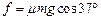
解得
设B物块释放后经t秒A追上B与其在斜面上相碰，由两者的位移关系得：
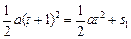
代入数据得：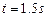
在此1.5s内，B物体下滑的位移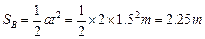
因为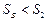
，AB确实是在斜面上发生碰撞。
（2）A碰前的速度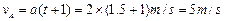
B碰前的速度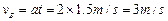
由于碰撞时间极短，两者碰撞近似动量守恒，设碰后两者的共同速度为v，则
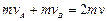
代入数据得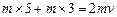
解得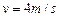
AB相碰时距斜面底端的高度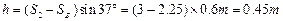
设AB滑下斜面后停在距P点S3远处。由动能定理得：
代入数据解得：
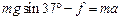
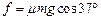
解得
设B物块释放后经t秒A追上B与其在斜面上相碰，由两者的位移关系得：
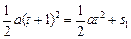
代入数据得：
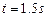
在此1.5s内，B物体下滑的位移
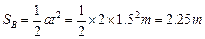
因为
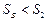，AB确实是在斜面上发生碰撞。（2）A碰前的速度
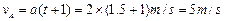
B碰前的速度
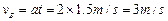
由于碰撞时间极短，两者碰撞近似动量守恒，设碰后两者的共同速度为v，则
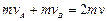
代入数据得
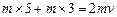
解得
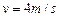
AB相碰时距斜面底端的高度
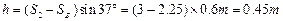
设AB滑下斜面后停在距P点S3远处。由动能定理得：
代入数据解得：
练习册系列答案
相关题目
的小球，绳AC长度为
，绳BC长度为
。求：
