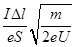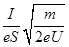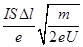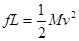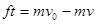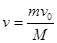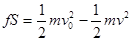题目内容
一个高尔夫球静止于平坦的地面上，在t=0时球被击出，飞行中球的速率与时间的关系如图所示．若不计空气阻力的影响，根据图象提供的信息可以求出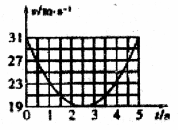
| A．高尔夫球在何时落地 |
| B．高尔夫球上升的最大高度 |
| C．人击球时对高尔夫球做的功 |
| D．高尔夫球落地时离击球点的距离 |
ABD
解析试题分析：高尔夫球做斜上抛运动，由图象可知，高尔夫球在5 s落地，选项A正确。根据机械能守恒定律有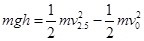
，可以计算高尔夫球上升的高度，选项B正确。人对高尔夫球做的功
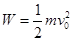，由于质量未知，选项C错误。在2.5 s是速度为19 m/s，这个速度就是在最高点时的水平速度，也是初速度的水平分量，在水平方向不受力，因此有
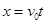，知道初速度和水平分速度，可知竖直方向的初速度分量v0y，再根据
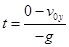计算出时间，高尔夫球落地时离击球点的距离x可求，选项D正确。
考点：本题考查曲线运动、机械能守恒定律、动能定理、速度的分解等。
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
如图12所示，π形光滑金属导轨与水平地面倾斜固定，空间有垂直于导轨平面的磁场，将一根质量为m的金属杆ab垂直于导轨放置。金属杆ab从高度h2处从静止释放后，到达高度为h1的位置（图中虚线所示）时，其速度为v，在此过程中，设重力G和磁场力F对杆ab做的功分别为WG和WF，那么
| A．mv2/2=mgh1－mgh2 |
| B．mv2/2=WG+WF |
| C．mv2/2>WG+WF |
| D．mv2/2<WG+WF |
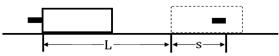
如图所示，固定位置在同一水平面内的两根平行长直金属导轨的间距为d，其右端接有阻值为R的电阻，整个装置处在竖直向上磁感应强度大小为B的匀强磁场中。一质量为m（质量分布均匀）的导体杆ab垂直于导轨放置，且与两导轨保持良好接触，杆与导轨之间的动摩擦因数为μ。现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离l时，速度恰好达到最大（运动过程中杆始终与导轨保持垂直）。设杆接入电路的电阻为r，导轨电阻不计，重力加速度大小为g。则此过程（ ）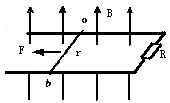
A．杆的速度最大值为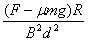 | B．流过电阻R的电量为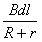 | C．恒力F做的功与摩擦力做的功之和等于杆动能的变化量 | D．恒力F做的功与安倍力做的功之和大于杆动能的变化量 |
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P，然后落回水平面．不计一切阻力．下列说法正确的是（ ）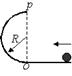
| A．小球落地点离O点的水平距离为2R |
| B．小球落地点时的动能为5mgR/2 |
| C．小球运动到半圆弧最高点P时向心力恰好为零． |
| D．若将半圆弧轨道上部的1/4圆弧截去，其他条件不变，则小球能达到的最大高度比P点高0.5R． |
在光滑的地板上，用水平拉力分别使两个物块由静止获得相同的动能，那么可以肯定（ ）
| A．水平拉力相等 | B．两物块质量相等 |
| C．两物块速度变化相等 | D．水平拉力对两物块做功相等 |
中国著名篮球运动员姚明在一次投篮中对篮球做功为W，出手高度为h1，篮筐距地面高度为h2，球的质量为m。不计空气阻力，则篮球进筐时的动能为( )
| A．W＋mgh1－mgh2 | B．mgh2－mgh1－W |
| C．mgh1＋mgh2－W | D．W＋mgh2－mgh1 |
