��Ŀ����
����Ŀ��(2016�����һģ)��ͼ��ˮƽ���ϵľ�����������һ���Ϊ���Ĺ̶�б�棬б���Ϸ�һ����Ϊm�Ĺ⻬��ֹʱ�����Ӷ�������Ӵ�����ѹ���������ɾ�ֹ��ʼ�������ȼ����˶���Ȼ�������ٶȴ�СΪa���ȼ����˶�ֱ����ֹ����������·��Ϊx���˶������е�����ٶ�Ϊv��
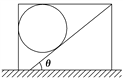
(1)�����Ӽ��ٽεļ��ٶ�Ϊa�䡣
(2)��a��gtan ��������ٽ����ܵ�������ںͶ�������������
���𰸡�(1)![]() ��(2)0����
��(2)0����![]() ��mg
��mg
��������������������˶�ѧ�Ĺ�ʽ�����������ļ��ٶȣ���������С���ܳ����������������ٽ��ٶȣ�Ȼ��ʹ�����巨�����ţ�ٵڶ����ɼ�����⡣
��1������ٶ�Ϊa�䣬���ȱ���ֱ���˶��Ĺ�ʽ�ɵ�
�ȼ���λ��Ϊ�� ![]() �ȼ���λ��Ϊ��
�ȼ���λ��Ϊ��![]()
λ�Ƽ�Ĺ�ϵΪ�� x��x1��x2
������ã� ![]()
��С���ܳ������������Ӧ������ˮƽ������Nsin ����ma
����ֱ����Ncos ����mg
������ã�a��gtan ��
����ʱ���ٶȵķ�������a��gtan �� ʱ����ڵ�֧��������0����ʱС���������ͼ��
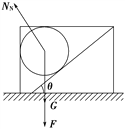
��ţ�ٵڶ����ɣ�Nsin ����ma�� ����ֱ������Ncos ����F��mg
������ã�![]()

��ϰ��ϵ�д�
�����Ŀ