题目内容
2.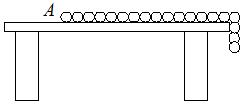 如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )| A. | $\frac{MLg}{50}$ | B. | $\frac{MLg}{10}$ | C. | $\frac{MLg}{250}$ | D. | $\frac{MLg}{25}$ |
分析 假设链条悬着的部分被拉回x时,拉力为F,根据牛顿第二定律求出F与x的关系,可知F与x是线性关系,再求F的平均值,由F的平均值与位移的乘积求F做的功.
解答 解:设链条悬着的部分被拉回x时,拉力为F,对整个链条,根据牛顿第二定律得:
F-$\frac{\frac{1}{5}L-x}{L}$Mg=M•0.1g
可得,F=0.3Mg-$\frac{x}{L}$Mg
则刚开始拉链条时,x=0,F1=0.3Mg
链条全部拉回桌面的瞬间,x=$\frac{1}{5}$L,代入F=0.3Mg-$\frac{x}{L}$Mg得 F2=0.1Mg
所以F的平均值为 $\overline{F}$=$\frac{{F}_{1}+{F}_{2}}{2}$=0.2Mg
拉力最少需做功 W=$\overline{F}$$\frac{L}{5}$=$\frac{MgL}{25}$
故选:D
点评 本题中拉力是变力,必须根据拉力的平均值求拉力做功,根据牛顿第二定律得到拉力与位移的关系是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
11.比较下列各物理量的大小时,正确的结论是( )
| A. | 电量:+2×10-8库仑>-3×10-8库仑 | |
| B. | 场强:+500牛顿/库仑>-800牛顿/库仑 | |
| C. | 电势:+60伏<-80伏 | |
| D. | 电势能:+48焦>-56焦 |
13. 如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )
如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )
 如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )
如图所示,A为多匝线圈,与电键、滑动变阻器相连之后,接入M、N间的恒定直流电源,B为一接有灵敏电流计的闭合多匝线圈,下列说法正确的是( )| A. | 保持电键闭合,灵敏电流计会一直有读数 | |
| B. | 断开电键后,再将B线圈靠近A线圈的过程中,灵敏电流计会发生偏转 | |
| C. | 闭合电键瞬间,灵敏电流计会发生偏转 | |
| D. | 保持电键闭合,将滑动变阻器的滑片左右移动过程中,灵敏电流计不会偏转 |
10.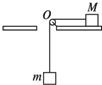 如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
 如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )| A. | 0.04 m | B. | 0.08 m | C. | 0.16 m | D. | 0.32 m |
7.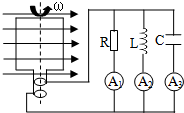 如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )
如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )
 如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )
如图,电阻不计的矩形线圈在匀强磁场中绕垂直于磁场的轴以ω的角速度匀速转动,此时三个电流表中的示数均为I,当线圈转动的角速度变为2ω时,电流表A1的示数为I1,电流表A2的示数为I2,电流表A3的示数为I3.则以下关系正确的是( )| A. | I1=2I | B. | I2=2I | C. | I3=2I | D. | I3>I1>I2 |
14.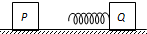 如图所示,质量均为m的小滑块P和Q都试作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的速度为多少?
如图所示,质量均为m的小滑块P和Q都试作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的速度为多少?
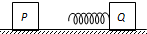 如图所示,质量均为m的小滑块P和Q都试作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的速度为多少?
如图所示,质量均为m的小滑块P和Q都试作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的速度为多少? 
 在“研究电磁感应现象”的实验中,所用的器材如图所示.
在“研究电磁感应现象”的实验中,所用的器材如图所示.