题目内容
10. 如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )
如图所示,在水平转台上放一个质量M=2kg的木块,它与转台间最大静摩擦力fmax=6.0N,绳的一端系在木块上,穿过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0kg的物体,当转台以角速度ω=5rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10m/s2,M、m均视为质点)( )| A. | 0.04 m | B. | 0.08 m | C. | 0.16 m | D. | 0.32 m |
分析 物体在随转台一起做匀速圆周运动,木块的重力摩擦力提供向心力,当摩擦力达到最大静摩擦力时,木块到O点的距离距离最大,根据向心力公式即可求解.
解答 解:物体的摩擦力和绳子的拉力的合力提供向心力,根据向心力公式得:
mg+f=Mω2r
解得:r=$\frac{mg+f}{M{ω}^{2}}$
当f=fmax=6.0N时,r最大,rmax=$\frac{10+6}{2×25}$=0.32m,
当f=-6N时,r最小,则rmin=$\frac{10-6}{50}$=0.08m;
故半径介于0.08m-0.32m之间,故BCD正确.
故选:BCD
点评 本题主要考查了向心力公式的直接应用,知道物体在随转台一起做匀速圆周运动,静摩擦力提供向心力,要注意明确静摩擦力的性质.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
19.下列情况中的运动物体,不能被看成质点的是( )
| A. | 研究飞往火星宇宙飞船的最佳运行轨道 | |
| B. | 调整人造卫星的姿态,使卫星的照相窗口对准地面 | |
| C. | 计算从北京开往上海的一列火车的运行时间 | |
| D. | 研究各大行星绕太阳公转的周期 |
1. 通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab与MN平行.关于MN的磁场对线框的作用,下列叙述中正确的是( )
通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab与MN平行.关于MN的磁场对线框的作用,下列叙述中正确的是( )
 通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab与MN平行.关于MN的磁场对线框的作用,下列叙述中正确的是( )
通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab与MN平行.关于MN的磁场对线框的作用,下列叙述中正确的是( )| A. | ab和cd两条边所受的安培力的方向相同 | |
| B. | 线框有两条边所受的安培力大小相等 | |
| C. | 线框受安培力的合力向右 | |
| D. | cd边所受安培力的方向向左 |
18.长为L的细线,一端固定在O点,另一端系一个小球,把小球拉到与悬点O处于同一水平面的A点,并给小球竖直向下的初速度,使小球绕O点在竖直平面内做圆周运动,要使小球能够在竖直平面内做竖直圆周运动,在A处小球竖直向下的最小速度应为( )
| A. | $\sqrt{3gL}$ | B. | $\sqrt{5gL}$ | C. | $\sqrt{7gL}$ | D. | $\sqrt{2gL}$ |
5.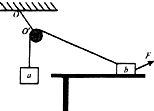 如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
 如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )| A. | 绳oo'的张力也在一定范围内变化 | |
| B. | 物块b所受到的支持力也在一定范围内变化 | |
| C. | 连接a和b的绳的张力也在一定范围内变化 | |
| D. | 物块b与桌面间的摩擦力保持不变 |
2.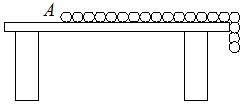 如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
 如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )| A. | $\frac{MLg}{50}$ | B. | $\frac{MLg}{10}$ | C. | $\frac{MLg}{250}$ | D. | $\frac{MLg}{25}$ |
20.物体受共点力F1、F2、F3作用而做匀速直线运动,则这三个力大小的可能值是( )
| A. | 15N,5N,16N | B. | 1N,2N,10N | C. | 3N,6N,4N | D. | 1N,6N,3N |