题目内容
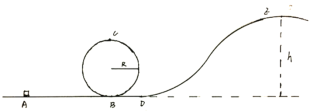
【题目】某游乐场的过山车可以抽象成如图所示的模型：半径为R=10m的光滑圆弧轨道下端与水平直线轨道相接于B点，曲线DE与AB相切于D点。总质量为m=1000kg的小车（自身安装有电动机）从直线轨道上A点以恒定的功率P=30kW开始加速，在直线轨道AB上经过t=30s其速度由零增加到最大，小车在直线轨道AB上所受阻力f=1000N，小车经过B点时关闭电动机并进入圆轨道，经C点返回B后再启动电动机进入光滑的BDE爬坡轨道，最终通过距离地面高度为h=50m的最高点E，不计空气阻力，重力加速度g取10m/s2。求：
(1)要使小车到达B点前速度达到最大，轨道AB的长度至少为多大？
(2)小车通过C点时对轨道的压力；
(3)要使小车能通过最高点E，电动机至少还要对小车做多少功？
【答案】(1)450m；(2)
；(3)
【解析】
(1)小车达到最大速度时，小车的牵引力等于阻力，则有
，
代入数据解得
若刚好到达B点达到最大速度，由功能关系得
代入数据解得
(2)小车经过B点时达到了最大速度
，从B到C，由功能关系可得
在C点，有
解得
由牛顿第三定律可知，小车通过C点时对轨道的压力
(3)要使小车恰好能通过最高点E，则从B到E，由功能关系得
解得电动机至少还要对小车多做的功
练习册系列答案
相关题目
