题目内容
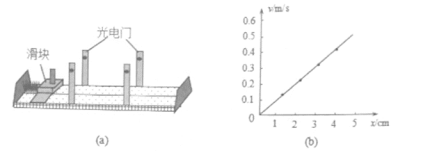
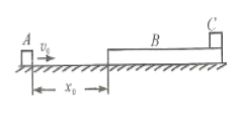
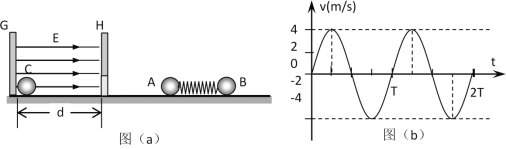
【题目】如图，光滑水平面上固定着一对竖直放置的平行金属板G和H。在靠近金属板G右壁固定一个可视为质点的小球C，其质量为 MC＝0.01kg、带电量为q＝＋1×10-5C。G、H两板间距离为d＝10cm，板H下方开有能让小球C自由通过的小洞。质量分别为MA＝0.01kg和MB＝0.02kg的不带电绝缘小球A、B用一轻质弹簧连接，并用细线栓连使弹簧处于压缩状态，静放在H板右侧的光滑水平面上，如图a所示。现将细线烧断，小球A、B在弹簧作用下做来回往复运动（A球不会进入G、H两板间）。以向左为速度的正方向，从烧断细线断开后的某时刻开始计时，得到A球的速度—时间图象如图(b)所示。
（1）求在
时刻小球B的速度，并在图(b)中大致画出B球的速度—时间图象；
（2）若G、H板间是电场强度为E=8×104V/m的匀强电场，在某时刻将小球C释放，则小球C离开电场时的速度为多大？
（3）若小球C以离开电场时的速度向右匀速运动，它将遇到小球A，并与之结合在一起运动，试定量分析在各种可能的情况下弹簧的最大弹性势能（即最大弹性势能的范围）。
【答案】(1)0，-2m/s ，2m/s，图见解析 （2）4m/s （3）0.02J—0.18J
【解析】
（1）对于小球A、B与轻质弹簧组成的系统，当烧断细线后动量守恒：
当
时有：
当
时有：
当
时有：
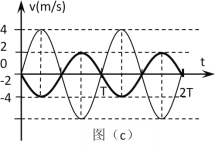
小球B的速度图象如图所示。
（2）当金属板间加有匀强电场时，电场力对小球做功，小球获得初动能并离开金属板，电场力做功：
由动能定理得：
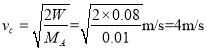
（3）因水平方向A、B、C三小球系统不受外力，故系统动量守恒。
由此可得：不论A、C两球何时何处相碰，三球的共同速度是一个定值，即三球速度相同时的总动能是一定值。
MCVC＝（MA＋MB＋MC）V共
解得
V共 ＝1m/s
当三球速度相同时弹簧的弹性势能最大。
当A球在运动过程中速度为4m/s且与C球同向时，跟C球相碰，系统损失能量最小（为0），此情况下三球在运动过程中弹簧具有的最大弹性势能设为E1
当A球在运动过程中速度为4m/s与C球反向时，跟C球相碰，系统损失能量最大，此情况下三球运动的过程中弹簧具有的最大弹性势能设为E2
解得
v3 =0
E2＝
（MA＋MC）v32＋MBvB2-（MA＋ MB＋MC）v共2＝0.02J
由上可得弹簧具有的最大弹性势能EPM的可能值在0.02J—0.18J的范围内。
