Question

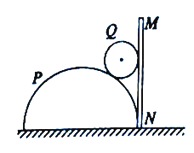
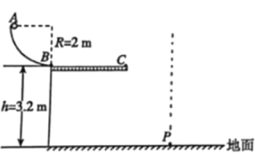
【题目】如图所示，一轨道由半径为2m的四分之一竖直圆弧轨道AB和长度L=3.5m的水平直轨道BC在B点平滑连接而成。现有一质量为0.2kg的滑块从A点无初速度释放，经过圆弧上B点时，传感器测得轨道所受压力大小为4.5N，然后经过水平直轨道BC，从C点水平飞离轨道，落到水平地面上的P点，P、C两点间的高度差为3.2m。滑块运动过程中可视为质点，且不计空气阻力。（g取10m/s2）

(1)求滑块运动至B点时的速度大小；

(2)若滑块与水平直轨道BC间的动摩擦因数μ0=0.3，求P、C两点的水平距离；

(3)在P点沿图中虚线安放一个竖直挡板，若滑块与水平直轨道BC间的动摩擦因数可调，问动摩擦因数取何值时，滑块击中挡板时的速度最小，并求此最小速度。

Answer 1

【答案】(1)5m/s；(2)1.6m；(3)，4m/s

【解析】

(1)在B点滑块做圆周运动，则有

解得

v=5m/s

(2)在BC段，滑块做匀减速运动，根据牛顿第二定律可知：

-μ0mg=ma

解得

由，解得

vC=2m/s

滑块从C点做平抛运动，则在竖直方向

解得

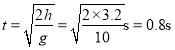
PC的水平位移为

x′=vCt=1.6m

(3)设BC间的摩擦因数为μ，则到达C点的速度为v′，则加速度大小为

a′=μg

根据，得

从C点做平抛运动，击中挡板所需时间为t′，则有

在竖直方向获得的速度为vy=gt′，击中挡板的速度为

当且仅当，v″取最小值，解得

，