��Ŀ����
��ͼ��ʾ���ڱڹ⻬��ľ������ΪmA=m����ֱ��Ϊ2L������ˮƽ�����ϣ����������Ķ�Ħ������Ϊ�̣�����������С��B��C�����ǵ������ֱ���mB=m��mC=2m���������̵ܶ��ᵯ��ѹ�������뵯�ɲ����ӣ�����B��ľ����ˡ�C��ľ���Ҷ˵ľ����ΪL����ʱ���ɵĵ�������ΪEP=��mgL��ͬʱ�ͷ�B��C������С�������ײ���룬��ײʱ�䲻�ƣ���
��1����1��С�������ײ��Ĺ�ͬ�ٶȣ�
��2����2��С�������ײ��Ĺ�ͬ�ٶȣ�
��3�������˶������У��������Ħ��������������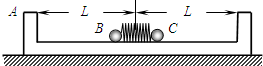
��1����1��С�������ײ��Ĺ�ͬ�ٶȣ�
��2����2��С�������ײ��Ĺ�ͬ�ٶȣ�
��3�������˶������У��������Ħ��������������

��1���ͷ�˲�䣺mBvB=mCvC
EP=
mBvB2+
mCvC2
��ã�vB=
vC=
����B��ʱ��t1=
=
����ľ��A��ײ
��mBvB=��mA+mB��v1��
��ã�v1��=
С�������ײ��Ĺ�ͬ�ٶ�Ϊ
��
��2��ľ��A��B����ײ��һ�������ȼ����˶������ٶ�a=
=2��g
ľ��A����B��ײ���ٶȼ�Ϊ0��ʱ��t2=
=
�ڣ�t1+t2�����ʱ���ڣ�����C�Ͳ��ƶ��ľ���֮��Ϊ��s=vC(t1+t2)+
v1��t2=
L��L������C ��A��ײǰA��ֹͣ�˶�
�پ���һ��ʱ�䣬��C��ľ����ײ���У�mCvC=��mA+mB+mC��v2��
���v2��=
������ˮƽ����
С�������ײ��Ĺ�ͬ�ٶ�Ϊ
������ˮƽ����
��3����һ����ײ��A��B���ܶ���ȫ��ת��ΪΪĦ����Q1=Ek1=
(mA+mB)v1��2=
��mgL
�ڶ�����ײ��ϵͳ���ܶ���ȫ��ת��ΪΪĦ����Q2=Ek2=
(mA+mB+mC)v2��2=
��mgL
���������������ľ����Ħ��������������ΪQ=Q1+Q2=
��mgL
�������Ħ����������Ϊ
��mgL��
EP=
| 1 |
| 2 |
| 1 |
| 2 |
��ã�vB=
|
vC=
|
����B��ʱ��t1=
| L |
| vB |
|
��mBvB=��mA+mB��v1��
��ã�v1��=
|
С�������ײ��Ĺ�ͬ�ٶ�Ϊ
|
��2��ľ��A��B����ײ��һ�������ȼ����˶������ٶ�a=
| ��(mA+mB+mC)g |
| mA+mB |
ľ��A����B��ײ���ٶȼ�Ϊ0��ʱ��t2=
| v1�� |
| a |
|
�ڣ�t1+t2�����ʱ���ڣ�����C�Ͳ��ƶ��ľ���֮��Ϊ��s=vC(t1+t2)+
| 1 |
| 2 |
| 3 |
| 4 |
�پ���һ��ʱ�䣬��C��ľ����ײ���У�mCvC=��mA+mB+mC��v2��
���v2��=
|
С�������ײ��Ĺ�ͬ�ٶ�Ϊ
|
��3����һ����ײ��A��B���ܶ���ȫ��ת��ΪΪĦ����Q1=Ek1=
| 1 |
| 2 |
| 1 |
| 3 |
�ڶ�����ײ��ϵͳ���ܶ���ȫ��ת��ΪΪĦ����Q2=Ek2=
| 1 |
| 2 |
| 1 |
| 6 |
���������������ľ����Ħ��������������ΪQ=Q1+Q2=
| 1 |
| 2 |
�������Ħ����������Ϊ
| 1 |
| 2 |

��ϰ��ϵ�д�
�����Ŀ
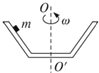 ��ͼ��ʾ���ڱڹ⻬��װ������ֱ��������ת����һ�����ڱڵ�С���壬������װ��һ����ˮƽ��������ת���Ĺ������������������ǣ�������
��ͼ��ʾ���ڱڹ⻬��װ������ֱ��������ת����һ�����ڱڵ�С���壬������װ��һ����ˮƽ��������ת���Ĺ������������������ǣ�������| A���»�������������Ħ���� | B������������������Ħ���� | C������������ | D�������������������� |
 ��ͼ��ʾ���ڱڹ⻬���������ڲͬ�߶ȴ���a��b����������Ϊm������ˮƽ����������Բ���˶���������
��ͼ��ʾ���ڱڹ⻬���������ڲͬ�߶ȴ���a��b����������Ϊm������ˮƽ����������Բ���˶��������� ��ͼ��ʾ���ڱڹ⻬��Բ̨�������̶�����������������ֱ����ʹһС���Ⱥ���M��N���������������ڱڷֱ���ͼ��������ʾ��ˮƽ����������Բ���˶�����С������
��ͼ��ʾ���ڱڹ⻬��Բ̨�������̶�����������������ֱ����ʹһС���Ⱥ���M��N���������������ڱڷֱ���ͼ��������ʾ��ˮƽ����������Բ���˶�����С������ ��2011?�Ӷ���һģ����ͼ��ʾ���ڱڹ⻬��ľ������ΪmA=m����ֱ��Ϊ2L������ˮƽ�����ϣ����������Ķ�Ħ������Ϊ�̣�����������С��B��C�����ǵ������ֱ���mB=m��mC=2m���������̵ܶ��ᵯ��ѹ�������뵯�ɲ����ӣ�����B��ľ����ˡ�C��ľ���Ҷ˵ľ����ΪL����ʱ���ɵĵ�������ΪEP=��mgL��ͬʱ�ͷ�B��C������С�������ײ���룬��ײʱ�䲻�ƣ���
��2011?�Ӷ���һģ����ͼ��ʾ���ڱڹ⻬��ľ������ΪmA=m����ֱ��Ϊ2L������ˮƽ�����ϣ����������Ķ�Ħ������Ϊ�̣�����������С��B��C�����ǵ������ֱ���mB=m��mC=2m���������̵ܶ��ᵯ��ѹ�������뵯�ɲ����ӣ�����B��ľ����ˡ�C��ľ���Ҷ˵ľ����ΪL����ʱ���ɵĵ�������ΪEP=��mgL��ͬʱ�ͷ�B��C������С�������ײ���룬��ײʱ�䲻�ƣ���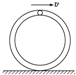 ��ͼ��ʾ���ڱڹ⻬�ĵ������Բ�ܹ����ֱ���ã�������Ϊ2m��С������Ϊm���ڹ��ڹ�������С���˶�����ߵ�ʱ�����ܸպ�Ҫ�뿪���森������뾶ΪR����
��ͼ��ʾ���ڱڹ⻬�ĵ������Բ�ܹ����ֱ���ã�������Ϊ2m��С������Ϊm���ڹ��ڹ�������С���˶�����ߵ�ʱ�����ܸպ�Ҫ�뿪���森������뾶ΪR����