题目内容
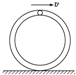如图所示，内壁光滑的导管弯成圆周轨道竖直放置，其质量为2m，小球质量为m，在管内滚动，当小球运动到最高点时，导管刚好要离开地面．（轨道半径为R）求：（1）球对管道作用力；
（2）此时小球的速度多大？
分析：当小球运动到最高点时，导管刚好要离开地面，知小球对管道的作用力等于管道的重力，结合牛顿第二定律求出小球的速度．
解答：解：（1）因为小球在最高点时，管道刚好离开地面，知地面的支持力为零，
根据共点力平衡得，球对管道的作用力F=2mg，方向竖直向上．
（2）根据牛顿第二定律得：mg+F=m
解得：v=
．
答：（1）球对管道的作用力大小2mg 方向竖直向上．
（2）此时小球的速度为
．
根据共点力平衡得，球对管道的作用力F=2mg，方向竖直向上．
（2）根据牛顿第二定律得：mg+F=m
| v2 |
| R |
解得：v=
| 3gR |
答：（1）球对管道的作用力大小2mg 方向竖直向上．
（2）此时小球的速度为
| 3gR |
点评：解决本题的关键知道小球做圆周运动向心力的来源，结合牛顿第二定律进行求解．
练习册系列答案
相关题目
如图所示在内壁光滑的锥形容器内侧不同高度处有a、b两球．质量均为m，都在水平面内做匀速圆周运动，则（ ）
如图所示，内壁光滑的圆台形容器固定不动，其轴线沿竖直方向．使一小球先后在M和N两处紧贴着容器内壁分别在图中虚线所示的水平面内做匀速圆周运动，则小球（ ）
（2011?河东区一模）如图所示，内壁光滑的木槽质量为mA=m，内直径为2L，置于水平桌面上，槽与桌面间的动摩擦因数为μ．槽内有两个小球B、C，它们的质量分别是mB=m，mC=2m．现用两球将很短的轻弹簧压紧（球与弹簧不连接），且B球到木槽左端、C球到木槽右端的距离均为L，这时弹簧的弹性势能为EP=μmgL．同时释放B、C球，并假设小球与槽碰撞后不分离，碰撞时间不计．求：
如图所示，内壁光滑的装置绕竖直轴匀速旋转，有一紧贴内壁的小物体，物体随装置一起在水平面内匀速转动的过程中所受外力可能是（ ）| A、下滑力、弹力、静摩擦力 | B、重力、弹力、滑动摩擦力 | C、重力、弹力 | D、重力、弹力、向心力 |