题目内容
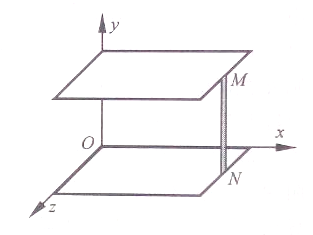
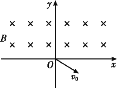
【题目】如图所示,在xOy平面内,第一、二象限有垂直纸面向里的相同的匀强磁场,第三、四象限有平行纸面的相同的匀强电场(未画出).一质量为m、电荷量为q的带正电的粒子,从坐标原点O以大小为v0、方向与x轴正方向成30°角的速度平行纸面斜向下射入第四象限,粒子首次回到x轴时,经过x轴上的P点且速度大小不变,已知O,P间距离为l,粒子重力不计。
(1)求匀强电场电场强度的大小和方向;
(2)如果粒子经磁场第一次偏转后,又恰好沿初始方向经过O点,求这时磁场的磁感应强度大小;
(3)如果第三、四象限的匀强电场电场强度变为原来的两倍,方向不变,其他条件不变,粒子经磁场偏转之后,经过电场,粒子能够再次通过O点,这时磁场的磁感应强度大小为多少。
【答案】(1) ![]() 垂直x轴,且沿y轴正方向 (2)
垂直x轴,且沿y轴正方向 (2) ![]() (3)
(3) ![]() (n=1,2,3,…)
(n=1,2,3,…)
【解析】
(1)根据题意可知,匀强电场垂直x轴,且沿y轴正方向.粒子在电场中沿OP方向匀速运动,有
l=v0tcos 30°
沿y轴负方向做匀减速运动有
Eq=ma
v0sin 30°=a![]()
解得
E=![]() .
.
(2)粒子从P点进入磁场时沿x轴方向速度分量不变,垂直x轴方向速度分量反向,因此粒子经过P点时的速度与x轴成30°角斜向上,经磁场第一次偏转后,又恰好经过O点,如图1中所示,由几何关系得
R=l
根据
qvB=m![]()
解得
B=![]()


(3)如果匀强电场电场强度大小变为原来的两倍,粒子在电场中沿x轴正方向匀速运动
l′=v0t′cos 30°
沿y轴负方向匀减速运动
2Eq=ma′
v0sin 30°=a′![]()
解得
l′=![]()
如果粒子经磁场偏转之后,其半径r<![]() ,粒子不可能过O点,如果粒子做圆周运动的半径r>
,粒子不可能过O点,如果粒子做圆周运动的半径r>![]() ,则每个周期粒子经过x轴的点将沿x轴负方向移动
,则每个周期粒子经过x轴的点将沿x轴负方向移动
Δx=r-![]()
如图2所示,带电粒子可能从电场再次经过O点需满足
![]() =nΔx (n=1,2,3,…)
=nΔx (n=1,2,3,…)
解得
r=![]() l(n=1,2,3,…)
l(n=1,2,3,…)
B′=![]() (n=1,2,3,…).
(n=1,2,3,…).