题目内容
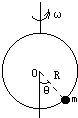 如图所示,竖直放置的光滑圆环,半径R=20厘米,在环上套有一个质量为m的小球,若圆环以ω=10弧度/秒的角速度转动,则角θ大小为( )
如图所示,竖直放置的光滑圆环,半径R=20厘米,在环上套有一个质量为m的小球,若圆环以ω=10弧度/秒的角速度转动,则角θ大小为( )分析:小球随圆环一起绕竖直轴转动,根据几个关系求出转动半径,再根据合外力提供向心力列方程求解.
解答:解:对小球进行受力分析,如图所示:
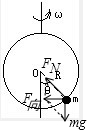
由几个关系得:小球转动半径为r=Rsinθ,tanθ=
根据向心力公式得:
F向=mω2r
所以mω2r=mgtanθ
带入数据解得:cosθ=
所以θ=60°
故选C.

由几个关系得:小球转动半径为r=Rsinθ,tanθ=
| F向 |
| mg |
根据向心力公式得:
F向=mω2r
所以mω2r=mgtanθ
带入数据解得:cosθ=
| 1 |
| 2 |
所以θ=60°
故选C.
点评:该题主要考查了向心力公式的直接应用,要求同学们能结合几何关系解题,注意小球转动半径不是R.

练习册系列答案
相关题目
 如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为
如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为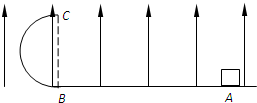 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小 如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )
如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( ) 物理选修3-3
物理选修3-3 如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求
如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求