题目内容
7. 在如图所示的电路中,电源电动势E=15V,内阻r=1Ω,R1=30Ω,R2=60Ω,滑动变阻器阻值为R,两平行金属板水平放置,板间距离d=20cm,g=10m/s2.
在如图所示的电路中,电源电动势E=15V,内阻r=1Ω,R1=30Ω,R2=60Ω,滑动变阻器阻值为R,两平行金属板水平放置,板间距离d=20cm,g=10m/s2.(1)当R=29Ω时,R2消耗的电功率是多少?
(2)若有一质量为2×10-3g,带电量为4×10-7C的油滴在两平行板之间恰好处于静止状态,则滑动变阻器连入电路中的电阻多大?
分析 (1)由电路图可知,R1与R2并联后与滑动变阻器串联,由串并联电路的性质可得出总电阻,由闭合电路欧姆定律可得电路中的电流及R2两端的电压,由功率公式P=$\frac{{U}^{2}}{R}$ 可求得R2消耗的电功率;
(2)对油滴由受力平衡:mg=q$\frac{U}{d}$,求得外压U,再由全电路欧姆定律求得R值.
解答 解:(1)闭合电路的外电阻为R外=R+$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$=49Ω ①
根据闭合电路的欧姆定律$I=\frac{E}{{R}_{外}+{r}_{0}}$ ②
R2两端的电压为U=E-I(r+R外)=(15-0.3×30)V=6V ③
R2消耗的功率为${P}_{2}=\frac{{U}^{2}}{{R}_{2}}$=0.6W ④
电阻R2消耗的电功率为0.6W;
(2)油滴受合力为0:mg=$\frac{U}{d}q$ ⑤
干路电流:I=$\frac{U}{\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}}$ ⑥
E=I(r+R+$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$) ⑦
由⑤⑥⑦可得:R=9Ω
答:(1)当R=29Ω时,R2消耗的电功率是0.6W
(2)滑动变阻器连入电路中的电阻为9Ω
点评 考查串联并联电路阻值的求解明确R=$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$,由受力平衡确定场强,由全电路欧姆定律定律E=u+Ir求得电阻.

| A. | 汽车经3s的速度大小为6m/s | B. | 汽车经3s的速度大小为4m/s | ||
| C. | 汽车经5s的速度大小为0m/s | D. | 汽车经6s的速度大小为2m/s |
 如图所示电路中,电阻R1的阻值发生变化,而其他电阻的阻值都保持不变,发现电压表V3的示数减小,由此可以判定( )
如图所示电路中,电阻R1的阻值发生变化,而其他电阻的阻值都保持不变,发现电压表V3的示数减小,由此可以判定( )| A. | 电压表V1的示数一定增大 | B. | 电压表V2的示数一定增大 | ||
| C. | 电阻R1的阻值一定增大 | D. | 电阻R1的阻值一定减小 |
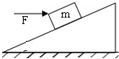 如图所示,一质量为m的物块在水平恒力F的作用下静止在粗糙的斜面上,若物块和斜面一直处于静止状态,下列说法中正确的是( )
如图所示,一质量为m的物块在水平恒力F的作用下静止在粗糙的斜面上,若物块和斜面一直处于静止状态,下列说法中正确的是( )| A. | 斜面对物块的作用力大小为$\sqrt{{F}^{2}+(mg)^{2}}$ | |
| B. | 物块一定受三个力作用 | |
| C. | 斜面与地面无摩擦力的作用 | |
| D. | 斜面与地面有摩擦力的作用,方向水平向左 |
 质量为5×103kg 的汽车从静止沿平直公路启动的速度与时间图象如图所示,A点表示匀加速的最后时刻,B点表示汽车达到最大速度,设汽车受恒定阻力,g=10m/s2,则( )
质量为5×103kg 的汽车从静止沿平直公路启动的速度与时间图象如图所示,A点表示匀加速的最后时刻,B点表示汽车达到最大速度,设汽车受恒定阻力,g=10m/s2,则( )| A. | 匀加速的加速度大小是0.5m/s | |
| B. | 阻力大小是1×104 N | |
| C. | 汽车的额定功率为3×10 5 w | |
| D. | 汽车从静止到达到最大速度时的总路程 337.5m |
 如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在 但A、B之间无弹力.已知重力加速度为g,某时刻细线剪断,则细线剪断瞬间,下列说法错误的是( )
如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在 但A、B之间无弹力.已知重力加速度为g,某时刻细线剪断,则细线剪断瞬间,下列说法错误的是( )| A. | 物块B的加速度为$\frac{1}{2}$g | B. | 物块A、B间的弹力为$\frac{1}{3}$mg | ||
| C. | 弹簧的弹力为$\frac{1}{2}$mg | D. | 物块A的加速度为$\frac{1}{3}$g |
 如图所示,一带电粒子,质量为m,带电荷量为q,仅受电场力作用,以恒定的速率v沿以圆弧做圆周运动,从圆弧上A点到B点速度方向改变了θ弧度,AB两点间弧长为s,则AB两点处电场强度的大小为$\frac{m{v}^{2}θ}{qs}$,AB两点间的电势差为0.
如图所示,一带电粒子,质量为m,带电荷量为q,仅受电场力作用,以恒定的速率v沿以圆弧做圆周运动,从圆弧上A点到B点速度方向改变了θ弧度,AB两点间弧长为s,则AB两点处电场强度的大小为$\frac{m{v}^{2}θ}{qs}$,AB两点间的电势差为0.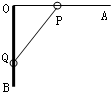 如图所示,直角支架的水平杆OA粗糙,竖直杆OB光滑,两个质量相同的小球P和Q分别套在OA和OB上,P和Q用不可伸长的轻绳连接,处于静止状态.若将小球P稍微向左移动少许后,P、Q仍静止.设杆对P的弹力为N,摩擦力为f,绳的张力为F,则与移动前相比较,下列说法正确的是( )
如图所示,直角支架的水平杆OA粗糙,竖直杆OB光滑,两个质量相同的小球P和Q分别套在OA和OB上,P和Q用不可伸长的轻绳连接,处于静止状态.若将小球P稍微向左移动少许后,P、Q仍静止.设杆对P的弹力为N,摩擦力为f,绳的张力为F,则与移动前相比较,下列说法正确的是( )