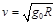题目内容
某人在一星球上以速度υ0竖直上抛一物体,设t秒钟后物体落回手里,已知星球的半径为R,那么至少要用多大的速度沿星球表面抛出,才能使物体不再落回星球表面?
小球做竖直上抛运动,则
由v0=g?
解得:g=
星球表面的小球所受重力等于星球对小球的吸引力,
则由mg=
得M=
现将此球沿此星球表面将小球水平抛出,欲使其不落回星球,则抛出时的速度至少为该星球的第一宇宙速度,
物体在星球表面附近能做匀速圆周运动,其向心力由星球的吸引力提供,
则由
=m
v=
=
=
.
答:至少要用
沿星球表面抛出,才能使物体不再落回星球表面.
由v0=g?
| t |
| 2 |
解得:g=
| 2v0 |
| t |
星球表面的小球所受重力等于星球对小球的吸引力,
则由mg=
| GMm |
| R2 |
得M=
| gR2 |
| G |
现将此球沿此星球表面将小球水平抛出,欲使其不落回星球,则抛出时的速度至少为该星球的第一宇宙速度,
物体在星球表面附近能做匀速圆周运动,其向心力由星球的吸引力提供,
则由
| GMm |
| R2 |
| v2 |
| R |
v=
|
| gR |
|
答:至少要用
|

练习册系列答案
相关题目