题目内容
如图所示的轨道由半径为R的1/4光滑圆弧轨道AB、竖直台阶BC、足够长的光滑水平直轨道CD组成.小车的质量为M,紧靠台阶BC且上水平表面与B点等高.一质量为m的可视为质点的滑块自圆弧顶端A点由静止下滑,滑过圆弧的最低点B之后滑到小车上.已知M=4m,小车的上表面的右侧固定一根轻弹簧,弹簧的自由端在Q点,小车的上表面左端点P与Q点之间是粗糙的,滑块与PQ之间表面的动摩擦因数为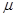 ,Q点右侧表面是光滑的.求:
,Q点右侧表面是光滑的.求:
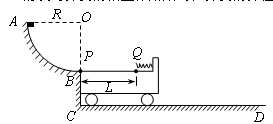
小题1:滑块滑到B点的瞬间对圆弧轨道的压力大小.
小题2:要使滑块既能挤压弹簧,又最终没有滑离小车,则小车上PQ之间的距离应在什么范围内?(滑块与弹簧的相互作用始终在弹簧的弹性范围内)
 ,Q点右侧表面是光滑的.求:
,Q点右侧表面是光滑的.求:
小题1:滑块滑到B点的瞬间对圆弧轨道的压力大小.
小题2:要使滑块既能挤压弹簧,又最终没有滑离小车,则小车上PQ之间的距离应在什么范围内?(滑块与弹簧的相互作用始终在弹簧的弹性范围内)
小题1:
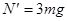
小题2:

(1)设滑块滑到B点的速度大小为v,到B点时轨道对滑块的支持力为N,由机械能守恒定律有
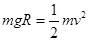 ① (2分) 高#考#资#滑块滑到B点时,由牛顿第二定律有
① (2分) 高#考#资#滑块滑到B点时,由牛顿第二定律有
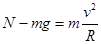 ② (2分)
② (2分)
联立①②式解得 N=3mg ③ (1分)
根据牛顿第三定律,滑块在B点对轨道的压力大小为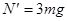 (1分)
(1分)
(2)滑块最终没有离开小车,滑块和小车必然具有共同的末速度设为u,滑块与小车组成的系统动量守恒,有
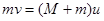 ④ (2分)
④ (2分)
若小车PQ之间的距离L足够大,则滑块可能不与弹簧接触就已经与小车相对静止,设滑块恰好滑到Q点,由功能关系有
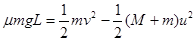 ⑤ (2分)
⑤ (2分)
联立①④⑤式解得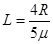 ⑥ (2分)
⑥ (2分)
若小车PQ之间的距离L不是很大,则滑块必然挤压弹簧,由于Q点右侧是光滑的,滑块必然被弹回到PQ之间,设滑块恰好回到小车的左端P点处,由功能关系有
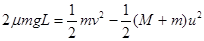 ⑦ (2分)
⑦ (2分)
联立①④⑦式解得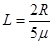 ⑧ (2分)
⑧ (2分)
综上所述并由⑥⑧式可知,要使滑块既能挤压弹簧,又最终没有离开小车,PQ之间的距离L应满足的范围是 ⑨ (2分)
⑨ (2分)
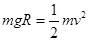 ① (2分) 高#考#资#滑块滑到B点时,由牛顿第二定律有
① (2分) 高#考#资#滑块滑到B点时,由牛顿第二定律有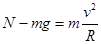 ② (2分)
② (2分)联立①②式解得 N=3mg ③ (1分)
根据牛顿第三定律,滑块在B点对轨道的压力大小为
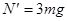 (1分)
(1分)(2)滑块最终没有离开小车,滑块和小车必然具有共同的末速度设为u,滑块与小车组成的系统动量守恒,有
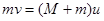 ④ (2分)
④ (2分)若小车PQ之间的距离L足够大,则滑块可能不与弹簧接触就已经与小车相对静止,设滑块恰好滑到Q点,由功能关系有
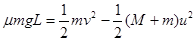 ⑤ (2分)
⑤ (2分)联立①④⑤式解得
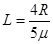 ⑥ (2分)
⑥ (2分)若小车PQ之间的距离L不是很大,则滑块必然挤压弹簧,由于Q点右侧是光滑的,滑块必然被弹回到PQ之间,设滑块恰好回到小车的左端P点处,由功能关系有
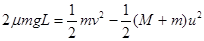 ⑦ (2分)
⑦ (2分)联立①④⑦式解得
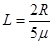 ⑧ (2分)
⑧ (2分)综上所述并由⑥⑧式可知,要使滑块既能挤压弹簧,又最终没有离开小车,PQ之间的距离L应满足的范围是
 ⑨ (2分)
⑨ (2分)
练习册系列答案
相关题目

 的初速度,使之向右运动,在木板与木块向右运动过程中,当木板和
的初速度,使之向右运动,在木板与木块向右运动过程中,当木板和 木块达到共速时,木板恰与墙壁相碰,碰撞过程时间极短,木板速度的方向改变,大小不变,最后木块恰好在木板的左端与木板相对静止。求:
木块达到共速时,木板恰与墙壁相碰,碰撞过程时间极短,木板速度的方向改变,大小不变,最后木块恰好在木板的左端与木板相对静止。求:
 ;
; ;
;