题目内容
(8分)如图所示，在倾角为θ的光滑斜面上，有一长为L的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在斜面上做完整的圆周运动，求：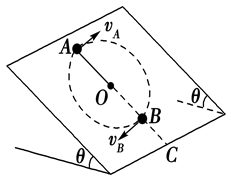
(1)小球通过最高点A时的速度vA.
(2)小球通过最低点B时，细线对小球的拉力．
(1)
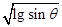(2) 6mgsinθ
解析试题分析：(1)小球恰好能在斜面上做完整的圆周运动，则小球通过A点时细线的拉力为零，根据圆周运动和牛顿第二定律有mgsinθ＝m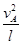
①
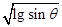解得：vA＝. ②
(2)小球从A点运动到B点，根据机械能守恒定律有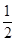
mvA2＋mg·2lsinθ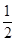＝mvB2③
解得vB＝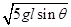
④
小球在B点时根据圆周运动和牛顿第二定律有FT－mgsinθ＝m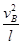
⑤
解得FT＝6mgsinθ. ⑥
考点：本题考查远中运动规律，机械能守恒定律和牛顿第二定律。
练习册系列答案
名校课堂系列答案
相关题目
的光滑半圆轨道竖直固定在高
的光滑水平台上，与平台平滑连接，平台长
.可视为质点的两物块
、
束缚在一起，并静止在平台的最右端D点，它们之间有被压缩的轻质弹簧，某时刻突然解除束缚，使两物块
，水平抛出后在水平地面上的落在水平地面上的P点，
，
取
．求：
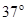的斜坡，BC是半径为
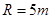的圆弧面，圆弧面和斜面相切于B，与水平面相切于C，如图所示，AB竖直高度差为
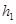，竖直台阶CD高度差为
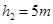，台阶底端与倾角为
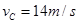，通过C点后飞落到DE上（不计空气阻力和轨道的摩擦阻力，
取10m/s2，sin37°=0.6，cos37°=0.8）．求：
？
？
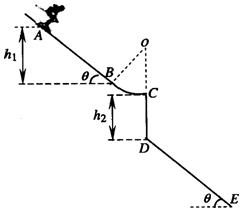
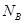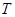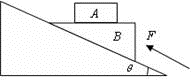
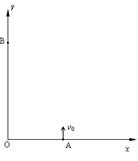
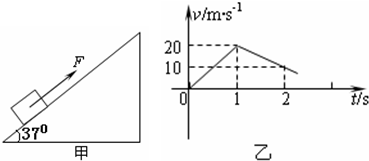
=37o，传送带AB长度xo=l0m。有一水平平台CD高度保持6．45m不变。现调整D端位置，当D、B的水平距离合适时，自D端水平抛出的物体恰好从B点沿BA方向冲上斜面，此后D端固定不动，g=l0m/s2。另外，传送带B端上方安装一极短的小平面，与传送带AB平行共面，保证自下而上传送的物体能沿AB方向由B点斜向上抛出。（sin37o=0．6，cos37o=0．8）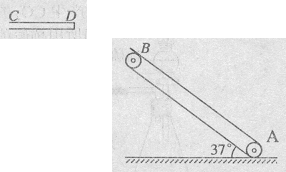
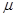1=0．9，自A点沿传送带方向以某一初速度冲上传送带时，恰能水平落到水平台的D端，求物体甲的最大初速度vo1
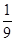×10－6C，如图所示，将小球B缓缓拉离竖直位置，当绳与竖直方向的夹角为60°时，将其由静止释放，小球B将在竖直面内做圆周运动．已知释放瞬间绳刚好张紧，但无张力．静电力常量
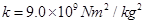，g取10m/s2。求