题目内容
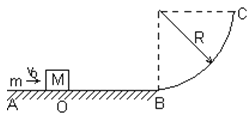
【题目】如图所示,AOB是光滑水平轨道,BC是半径为R的1/4光滑圆弧轨道,两轨道恰好相切。质量为M的小木块静止在O点,一质量为m (m = M/9) 的子弹以某一初速度水平向右射入小木块内不穿出,木块恰好滑到圆弧的最高点C处(子弹、小木块均可看成质点)。求:
(1)子弹射入木块之前的速度vo多大?
(2)若每当小木块在O点时,立即有相同的子弹以相同的速度vo射入小木块,并留在其中,则当第6颗子弹射入小木块后,小木块沿光滑圆弧上升的高度h是多少?
【答案】(1)![]() (2)0
(2)0
【解析】
(1)木块由O上滑到C过程中,机械能守恒,由机械能守恒定律
![]()
子弹射入木块过程系统动量守恒,由动量守恒定律得
mv0=(M+m)v
解得
![]()
(2)木块回到O点时的动量与第2颗子弹射入木块前的动量等大反向,子弹和木块组成的系统总动量为零,射入子弹的颗数n=2、4、6、8…时系统总动量都为零,由动量守恒定律可知,子弹打入后系统的速度为零,木块静止,木块上升的高度h=0。

练习册系列答案
相关题目