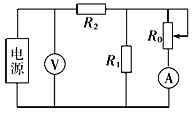
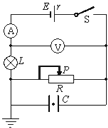
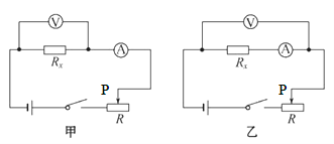
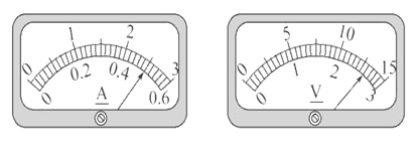
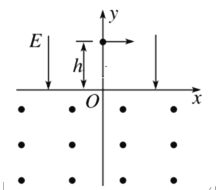
题目内容
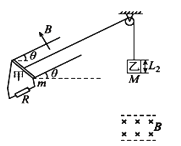
【题目】如图所示，两根足够长的固定平行光滑金属导轨间的距离L1=1m，导轨平面与水平面的夹角θ=
，整个导轨平面内存在垂直于导轨平面斜向上的匀强磁场，磁感应强度大小B=0.5T，在导轨的底端连接一个阻值为R=0.5Ω的电阻．一根质量m=1kg、电阻不计、垂直于导轨放置的金属棒甲通过平行于导轨平面的绝缘轻绳和一个质量M=1kg、边长L2=0.8m、电阻r=0.32Ω的正方形线框乙相连，轻绳绕过固定在天花板的光滑轻质定滑轮．线框乙下方存在磁感应强度大小也为B=0.5T的有界匀强磁场，线框乙的下边距离磁场的上边界h=4.8m，磁场宽度大于线框边长．开始时用外力作用于金属棒甲，使整个系统处于静止状态，然后撤去外力，系统从静止开始运动，线框乙进入磁场时恰好做匀速运动．已知g=10m/s2，sin=0.6，cos=0.8，求：
（1）线框乙刚开始运动时轻绳对金属棒甲的拉力大小；
（2）线框乙刚进入磁场时的速度大小以及从开始释放到线框乙刚进入磁场的过程中电阻R上产生的焦耳热；
（3）线框乙从刚开始进入到完全进入磁场的过程中，线框乙中产生的焦耳热．
【答案】（1）8N；（2）4m/s， 3.2J；（3）1.6J．
【解析】
(1)设线框乙刚开始运动时轻绳对金属棒甲的拉力大小为F，系统刚释放的瞬间，线框乙和金属棒甲均无速度，故二者均不受安培力作用．分别对线框乙和金属棒甲受力分析，由牛顿第二定律得
MgF=Ma
Fmgsinθ=ma
代入数据解得
F=8N
(2)当线框乙刚进入磁场时，线框乙和金属棒甲均做匀速运动，设此时系统的速度为v，系统处于平衡状态，对线框乙：线框乙底边切割磁感线产生的电动势E2=BL2v，线框乙中流过的电流
线框乙受到的安培力F2=BI2L2，设此时绳中的张力为T，对线框乙由平衡条件得
Mg=T+F2
对金属棒甲：金属棒甲切割磁感线产生的电动势E1=BL1v，回路中流过的电流
金属棒甲受到的安培力F1=BI1L1，对金属棒甲由平衡条件得
mgsinθ+F1=T
解得
v=4m/s
对系统由能量守恒定律得
(Mgmgsinθ)h=E0+
(m+M)v2
解得电阻R上产生的焦耳热为
E0=3.2J
(3)线框乙从刚进入磁场到完全进入磁场的过程中，系统做匀速运动，电流恒定，安培力恒定，故此过程运动的时间为
线框乙中产生的焦耳热为
Q=
rt=1.6J
