Question

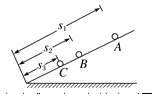
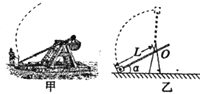
【题目】如图甲所示，在直角坐标系中的0≤x≤L区域内有沿y轴正方向的匀强电场，右侧有以点（2L，0）为圆心、半径为L的圆形区域，与x轴的交点分别为M、N，在xOy平面内，从电离室产生的质量为m、带电荷量为e的电子以几乎为零的初速度从P点飘入电势差为U的加速电场中，加速后经过右侧极板上的小孔Q点沿x轴正方向进入匀强电场，已知O、Q两点之间的距离为，飞出电场后从M点进入圆形区域，不考虑电子所受的重力。

（1）求0≤x≤L区域内电场强度E的大小和电子从M点进入圆形区域时的速度vM；

（2）若圆形区域内加一个垂直于纸面向外的匀强磁场，使电子穿出圆形区域时速度方向垂直于x轴，求所加磁场磁感应强度B的大小和电子在圆形区域内运动的时间t；

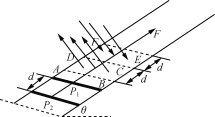
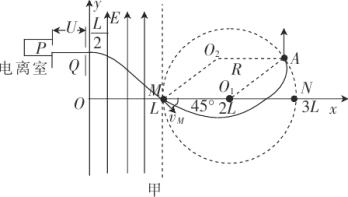
（3）若在电子从M点进入磁场区域时，取t＝0，在圆形区域内加如图乙所示变化的磁场（以垂直于纸面向外为正方向），最后电子从N点飞出，速度方向与进入圆形磁场时方向相同，请写出磁场变化周期T满足的关系表达式。

Answer 1

【答案】（1），，设vM的方向与x轴的夹角为θ，θ＝45°；（2），；（3）T的表达式为（n＝1，2，3，…）

【解析】

（1）在加速电场中，从P点到Q点由动能定理得：

可得

电子从Q点到M点，做类平抛运动，

x轴方向做匀速直线运动，

y轴方向做匀加速直线运动，

由以上各式可得：

电子运动至M点时：

即：

设vM的方向与x轴的夹角为θ，

解得：θ＝45°。

（2）如图甲所示，电子从M点到A点，做匀速圆周运动，因O2M＝O2A，O1M＝O1A，且O2A∥MO1，所以四边形MO1AO2为菱形，即R＝L

由洛伦兹力提供向心力可得：

即

。

（3）电子在磁场中运动最简单的情景如图乙所示，在磁场变化的半个周期内，粒子的偏转角为90°，根据几何知识，在磁场变化的半个周期内，电子在x轴方向上的位移恰好等于轨道半径，即

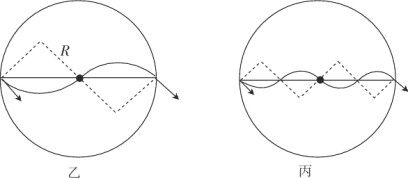
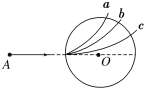
因电子在磁场中的运动具有周期性，如图丙所示，电子到达N点且速度符合要求的空间条件为：（n＝1，2，3，…）

电子在磁场中做圆周运动的轨道半径

解得：（n＝1，2，3，…）

电子在磁场变化的半个周期内恰好转过圆周，同时在MN间的运动时间是磁场变化周期的整数倍时，可使粒子到达N点且速度满足题设要求，应满足的时间条件是

又

则T的表达式为（n＝1，2，3，…）。