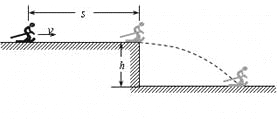
题目内容
【题目】一质量为M=2kg的长木板在粗糙水平地面上运动，在t=0时刻，木板速度为v0=12m/s，此时将一质量为m=1kg的小物块（可视为质点）无初速度地放在木板的右端，二者在0～2s内运动的v﹣t图象如图所示．己知重力加速度g=10m/s2．求：
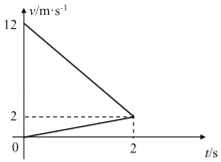
（1）小物块与木板的动摩擦因数μ1，以及木板与地面间的动摩擦因数μ2．
（2）小物块最终停在距木板右端多远处？
（3）若在t=2s时．使小物块的速度突然反向（大小不变），小物块恰好停在木板的左端，求木板的长度L．
【答案】（1）0.1， 0.3．（2）10.5m．（3）14.4m．
【解析】（1）小物块的加速度：a1=
，
长木板的加速度：a2=
，
对小物块受力分析，受重力、支持力和滑动摩擦力，根据牛顿第二定律，有：μ1mg=ma1，
木板水平方向受滑块向后的摩擦力和地面向后的摩擦，根据牛顿第二定律，有：﹣μ1mg﹣μ2（M+m）g=Ma2，
μ1=0.1，μ2=0.3；
（2）v﹣t图象与时间轴包围的面积表示位移大小，2s内相对位移大小：
△x1=
；
m受摩擦力：f1=μ1mg=1N，
M受地面的滑动摩擦力：f2= 
=9N，
2s后M与m均是减速，但M加速度小于m的加速度，分别为：
2s后M的位移： 
，
2s后m的位移： 
2s后m相对于M的位移：△x′=xm﹣xM=2﹣0.5=1.5m；
故小物块最终停在距木板右端：△x1﹣△x′=12﹣1.5=10.5m；
（3）若在t=2s时．使小物块的速度突然反向，则m受向后的摩擦力，一直到速度减小为零；M受向左的两个摩擦力，一直到速度减为零；
m的加速度： 
M的加速度： 
对m，位移： 
对M，位移： 
，
故2s后的相对位移大小：△x″=x1+x2=2.4m，
故木板的长度L=△x″+△x1=2.4+12=14.4m；
