Question

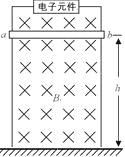
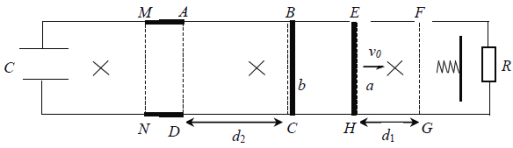
【题目】如图所示，有两光滑平行金属导轨，导轨的间距l=1m，左侧接C=0.1F的电容，右侧接的电阻，中间MA、ND段光滑绝缘，ABCD区域、EFGH区域、MN左侧均存在垂直于平面，磁感应强度B=1T的匀强磁场，EFGH区域、ABCD区域的宽度分别为，，FG的右侧固定一轻质弹簧。质量均为m=0.1kg金属杆a、b，金属杆a以速度的速度进入EFGH区域磁场，金属杆b静止在ABCD区域外侧，金属杆a、b的电阻分别为、，金属杆a、b之间的碰撞均为弹性碰撞，求：

（1）金属杆a刚进入磁场时，受到的安培力大小；

（2）全过程金属杆a上产生的焦耳热；

（3）电容器最终的带电量。

Answer 1

【答案】（1）；（2）1.87J；（3）0.1C

【解析】

（1）电源电动势

电阻R与r2并联，总电阻

（2）金属杆a通过EFGH区域：

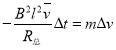
金属杆a通过与弹簧碰撞以v=8m/s反弹，经过EFGH区域速度再减掉2m/s，变成

金属杆a、b发生弹性碰撞，满足：

动量守恒

能量守恒

求得金属杆b的速度为

金属杆b通过ABCD区域，电路发生改变：

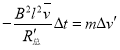
金属杆a切割产生的总焦耳热

金属杆a分配到1.6J

金属杆b切割产生的总焦耳热

金属杆a分配到

总共产生了1.87J的热

（3）金属杆b进入左侧电容区域，最终金属杆b两端电压和电容器两端电压相等时，匀速。此时速度设为v．电容器上的电量和流过的电量金属杆b相等，设为q

且

求得：q=0.1C