题目内容
7.假设月球和地球同步卫星都绕地心做匀速圆周运动.下列说法中正确的是( )| A. | 地球同步卫星的线速度小于月球的线速度 | |
| B. | 地球同步卫星的角速度小于月球的角速度 | |
| C. | 地球同步卫星的向心加速度小于月球的向心加速度 | |
| D. | 地球同步卫星的轨道半径小于月球的轨道半径 |
分析 根据万有引力提供向心力得出线速度、角速度、周期、向心加速度与轨道半径的关系,通过周期的大小比较轨道半径的大小,从而比较线速度、角速度、向心加速度的大小.
解答 解:根据$G\frac{Mm}{{r}^{2}}=ma=m\frac{{v}^{2}}{r}=mr{ω}^{2}$=$mr\frac{4{π}^{2}}{{T}^{2}}$得,$a=\frac{GM}{{r}^{2}}$,$v=\sqrt{\frac{GM}{r}}$,$ω=\sqrt{\frac{GM}{{r}^{3}}}$,T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,
因为月球的周期大于同步卫星的周期,则月球的轨道半径大于同步卫星的轨道半径,故D正确.
地球同步卫星的轨道半径小,则线速度大,角速度大,向心加速度大,故A、B、C错误.
故选:D.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,知道线速度、角速度、周期、向心加速度与轨道半径的关系.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
17.某物体运动的v-t图象如图所示,下列说法正确的是( )
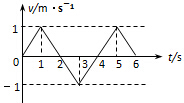

| A. | 物体在第1 s末运动方向发生改变 | |
| B. | 物体在第2 s内和第4 s内的加速度是相同的 | |
| C. | 物体在第4 s末返回出发点 | |
| D. | 物体在第5 s时离出发点最远,且最大位移为0.5 m |
18.如图所示能使原来不带电的导体A、B带电的实验所采用的起电方式为( )


| A. | 摩擦起电 | B. | 接触起电 | C. | 感应起电 | D. | 以上都不对 |
16.关于力的下列各种说法中,不正确的是( )
| A. | 力是改变物体的运动状态的原因 | |
| B. | 力是产生形变的原因 | |
| C. | 只有相互接触的物体才有力的作用 | |
| D. | 在国际单位制中,力的单位是牛顿,简称牛,符号为N |



