ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ‘ΎΧλΜ®Αε…œΙΧΕ®ΝΫΗωΙβΜ§ΒΡΕ®Μ§¬÷Θ§ΫΪ“ΜΒΦ»»–‘ΡήΝΦΚΟΒΡ‘≤Ά≤Ζ≈‘ΎΥ°ΤΫΒΊΟφ…œΘ§‘≤Ά≤ΒΡΑκΨΕΈΣRΘ§œ÷”Ο“ΜΑκΨΕ“≤ΈΣRΒΡ÷ ΝΩΈΣm1ΒΡΜν»ϊΖβ±’ΝΥ“ΜΕ®÷ ΝΩΒΡΤχΧεΘ§»ΜΚσ”Ο“Μ÷ ΝΩ≤ΜΦΤΒΡ«α…ΰΩγΙΐΝΫΙβΜ§ΒΡΕ®Μ§¬÷”κ÷ ΝΩΈΣm2ΒΡΙ≥¬κΚΆΜν»ϊœύΝ§Ϋ”ΓΘΨ≠≤βΝΩΆβΫγΒΡΜΖΨ≥Έ¬Ε»ΈΣTΘ§Μν»ϊΨύάκ‘≤Ά≤ΒΉ≤ΩΒΡΦδΨύΈΣl0Θ§ΦΌ…ηΚω¬‘“Μ«–ΡΠ≤ΝΘ§Μν»ϊ”κ‘≤Ά≤ΒΡΖβ±’ΝΦΚΟΘ§Ζβ±’ΒΡΤχΧεΩ… ”ΈΣάμœκΤχΧεΘ§÷ΊΝΠΦ”ΥΌΕ»»ΓgΓΘ«σΘΚ
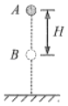
Θ®1Θ©Β±ΜΖΨ≥ΒΡΈ¬Ε»ΜΚ¬ΐΒΊΫΒΈΣT/2Θ§¥ΐΉΑ÷ΟΤΫΚβ ±Μν»ϊάκ‘≤Ά≤ΒΉΒΡΗΏΕ»hΓδ”ΠΈΣΕύ¥σΘΩ
Θ®2Θ©»γΙϊ±Θ≥÷ΫΒΒΆΚσΒΡΈ¬Ε»T/2Θ§‘Ύ”“≤ύ‘ΌΦ”÷ ΝΩΈΣΓςmΒΡΙ≥¬κΘ§¥ΐ‘Ό¥ΈΤΫΚβ ±Θ§Μν»ϊΨύάκ‘≤Ά≤ΒΉ≤ΩΒΡΨύάκΈΣl0Θ§«σΆβΫγ¥σΤχ―Ι«Ωp0”ΠΈΣΕύ¥σΘΩ
ΓΨ¥πΑΗΓΩΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]()
ΓΨΫβΈωΓΩ
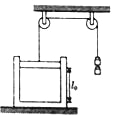
ΔΌ…η‘Ό¥ΈΤΫΚβ ±ΓΘΜν»ϊΒΫΤχΗΉΒΉΒΡΗΏΕ»ΈΣh1Θ§ΜΖΨ≥Έ¬Ε»ΜΚ¬ΐΫΒΒΆΙΐ≥Χ÷–ΤχΗΉ÷–ΤχΧε―Ι«Ω≤Μ±δΘ§ΤχΗΉΒΡΚαΫΊΟφΜΐΘΚS=Π–R2ΓΘ
≥θΧ§ΘΚΈ¬Ε»T1=TΘ°ΧεΜΐV1=l0S
Ρ©Χ§ΘΚΈ¬Ε»T2=T/2Θ°ΧεΜΐV2=hΓδS
ΗυΨίΗ«©¹¬ά»χΩΥΕ®¬…Ω…ΒΟΘΚ![]()
Ω…ΒΟΜν»ϊ”κΗΉΒΉΒΡΨύάκΘΚhΓδ=![]() l0
l0
ΔΎ…η¥σΤχ―Ι«ΩΈΣp0Θ§
≥θΧ§ΘΚ―Ι«Ω![]() Θ§ΧεΜΐ
Θ§ΧεΜΐ![]()
Ρ©Χ§ΘΚ―Ι«Ω![]() Θ§ΧεΜΐΘΚV3=h2S
Θ§ΧεΜΐΘΚV3=h2S
”…Β»Έ¬±δΜ·ΘΚp2V2=p3V3
Ω…ΒΟΘΚP0=![]()