题目内容
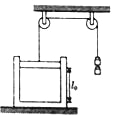
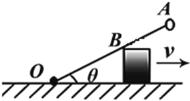
【题目】如图所示，一根长为l的轻杆OA，O端用铰链固定，另一端固定着一个小球A，轻杆靠在一个高为h的物块上.若物块与地面摩擦不计，则当物块以速度v向右运动至杆与水平方向夹角为θ时，物块与轻杆的接触点为B，下列说法正确的是（ ）
A. A、B的线速度相同
B. A、B的角速度不相同
C. 轻杆转动的角速度为
D. 小球A的线速度大小为
【答案】C
【解析】
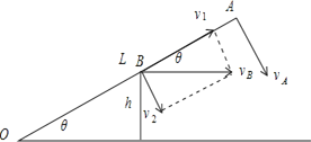
根据运动的合成与分解可知，接触点B的实际运动为合运动，可将B点运动的速度vB=v沿垂直于杆和沿杆的方向分解成v2和v1，其中v2=vBsinθ= vsinθ为B点做圆周运动的线速度，v1=vBcosθ= vcosθ为B点沿杆运动的速度，如图所示．
A、当杆与水平方向夹角为θ时，
；A、B两点都围绕O点做圆周运动，由于同一杆上运动，故角速度ω相同，由于转动半径不一样，故A、B的线速度不相同，故A错误；
B、由于A、B在同一杆上绕O点做圆周运动，故A、B绕O做圆周运动的角速度相同，故B错误；
C、由于B点的线速度为v2=vsinθ=OBω，所以
，故C正确；
D、由角速度和线速度的关系可知，A的线速度
，故D错误．
故选C.
练习册系列答案
名校课堂系列答案
相关题目
