题目内容
如图，质量为M的顶部有竖直壁的容器，置于倾角为θ的固定光滑斜面上，底部与斜面啮合，容器顶面恰好处于水平状态，容器内有质量为m的光滑小球与右壁接触。让M、m系统从斜面上端由静止开始下滑L后刚好到达斜面底端。（重力加速度为g）求：
（1）系统到达斜面底端的速度大小
（2）下滑过程中，m超重还是失重？ M水平顶面对m的支持力大小为多少？
（3）下滑过程中，M对m所做的功。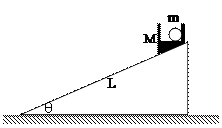
（1）系统到达斜面底端的速度大小
（2）下滑过程中，m超重还是失重？ M水平顶面对m的支持力大小为多少？
（3）下滑过程中，M对m所做的功。
（1）
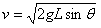（2）mgcos2θ（3）0
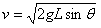（2）mgcos2θ（3）0（1）根据机械能守恒定律：
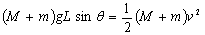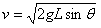解得：…（4分）
（2）下滑过程中m失重。……………………………………………（3分）
小球与容器一起沿斜面自由下滑，加速度为a=gsinθ。…………（1分）
如图竖直方向受mg、N向下加速，根据牛顿第二定律：
mg－N=masinθ …………………………………………………（3分）
代入a=gsinθ解得N=mg（1－sin2θ）=mgcos2θ………………（1分）
（3）对小球根据动能定理：
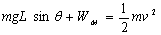………………………………………（2分）
解得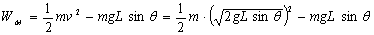
=0…（2分）
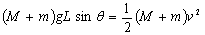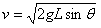解得：…（4分） （2）下滑过程中m失重。……………………………………………（3分）
小球与容器一起沿斜面自由下滑，加速度为a=gsinθ。…………（1分）
如图竖直方向受mg、N向下加速，根据牛顿第二定律：mg－N=masinθ …………………………………………………（3分）
代入a=gsinθ解得N=mg（1－sin2θ）=mgcos2θ………………（1分）
（3）对小球根据动能定理：
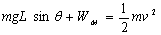………………………………………（2分）解得
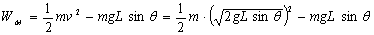=0…（2分）
练习册系列答案
阅读快车系列答案
相关题目
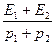
圆弧，半径为R，BC段水平且长度为R，一小物块质量为m与轨道间动摩擦因数为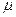
．当它从轨道顶端A无初速下滑时，恰好运动到C点静止，求：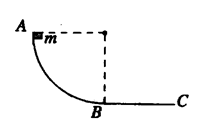
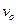至少应为多大？
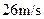，那么，摩托车飞离高台时的最大速度
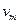应为多少？
和动能Eka；
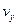和动能Eky；
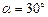，导轨上端跨接一定值电阻R=1.6
，导轨电阻不计.整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1.0T的匀强磁场中，金属棒ef垂直于MN、PQ静止放置，且与导轨保持良好接触，其长刚好为d、质量度m=0.10kg、电阻r=0.40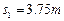
。另一根与金属棒平行放置的绝缘棒gh长度也为d，质量为m/2，从轨道最低点以速度
沿轨道上滑并与金属棒发生正碰（碰撞时间极短），碰后金属棒沿导轨上滑
后再次静止。测得从碰撞至金属棒静止过程中电阻R上产生的焦耳热为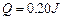
。已知两棒与导轨间的动摩擦因数均为
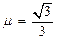，取
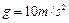，求：
