题目内容
【题目】如图所示,在粗糙水平面上A点固定一半径R=0.2m的竖直光滑圆弧轨道,底端有一小孔.在水平面上距A点s=1m的B点正上方O处,用长为L=0.9m的轻绳悬挂一质量M=0.1kg的小球甲,现将小球甲拉至图中C位置,绳与竖直方向夹角![]() =60°.静止释放小球甲,摆到最低点B点时与另一质量m=0.05kg的静止小滑块乙(可视为质点)发生完全弹性碰撞.碰后小滑块乙在水平面上运动到A点,并无碰撞地经过小孔进入圆弧轨道,当小滑块乙进入圆轨道后立即关闭小孔.g=10m/s2 .
=60°.静止释放小球甲,摆到最低点B点时与另一质量m=0.05kg的静止小滑块乙(可视为质点)发生完全弹性碰撞.碰后小滑块乙在水平面上运动到A点,并无碰撞地经过小孔进入圆弧轨道,当小滑块乙进入圆轨道后立即关闭小孔.g=10m/s2 .
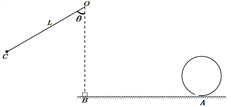
(1)求甲、乙碰前瞬间小球甲的速度大小;
(2)若小滑块乙进入圆轨道后的运动过程中恰好不脱离圆弧轨道,求小滑块乙与水平面的动摩擦因数![]() .
.
【答案】(1)3m/s(2)0.6
【解析】(1)小球甲由C到B,由动能定理得
![]() ①
①
![]() ②
②
(2)甲乙发生弹性碰撞
![]() ③
③
![]() ④
④
![]() m/s ⑤
m/s ⑤
若小球恰能经过最高点,则最高点速度![]() 满足
满足
![]() ⑥
⑥
![]() ⑦
⑦
从B到圆弧最高点,由动能定理有
![]() ⑧
⑧
![]() ⑨
⑨
若不能转过圆轨道最高点,则最高点必在圆心
![]() ⑩
⑩
![]()

练习册系列答案
相关题目