题目内容
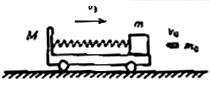
如图所示,光滑水平面上有一质量M=1.0kg的小车,小车右端有一个质量m=0.90kg的滑块,滑块与小车左端的挡板之间用轻弹簧相连接,滑块与车面间的动摩擦因数μ=0.20,车和滑块一起以v1=10m/s的速度向右做匀速直线运动,此时弹簧为原长。质量m0=0.10kg的子弹,以v0=50m/s的速度水平向左射入滑块面没有穿出,子弹射入滑块的时间极短。当弹簧压缩量d=0.50m,重力加速度g=10m/s2,求:
(1)子弹与滑块刚好相对静止的瞬间,子弹与滑块共同速度的大小和方向;
(2)弹簧压缩到最短时,小车的速度大小和弹簧的弹性势能;
(3)如果当弹簧压缩到最短时,不锁定弹簧,则弹簧再次回到原长时,车的速度大小.
解:
(1)设子弹和滑块相对静止时共同速度为v,根据动量守恒定律
![]()
解得:v=4.0m/s
方向向右
(2)设弹簧压缩到最短时它们的共同速度为![]() ,根据动量守恒定律
,根据动量守恒定律
![]()
设滑块与车摩擦产生的热为Q,弹簧的最大弹性势能为EP,根据能量守恒有:
![]()
![]()
(3)设弹簧再次回到原长时,车的速度为v1,滑块(和子弹)的速度为v2,根据动量守恒定律
![]()
根据能量守恒:
![]()
解得:车的速度大小为![]()
(另一解![]() 舍去)
舍去)

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求: 如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )
如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )