题目内容
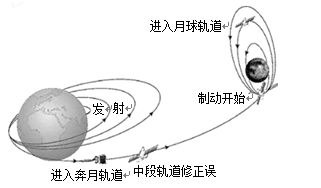
图示是我国的“探月工程”向月球发射一颗绕月探测卫星“嫦娥一号”过程简图．“嫦娥一号”进入月球轨道后，在距离月球表面高为h的轨道上绕月球做匀速圆周运动．
（1）若已知月球半径为R月，月球表面的重力加速度为g月，则“嫦娥一号”环绕月球运行的周期为多少？
（2）若已知R月=
R地，g月=
g地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？
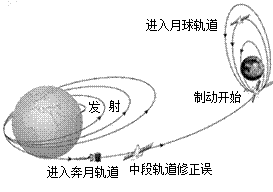
（1）设“嫦娥一号”环绕月球运行的周期是T，根据牛顿第二定律得
G
= mg月 （2分）
G
= m
（R月+h）（2分）
解得T=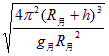
（2分）
（2）对于靠近天体表面的行星或卫星有mg=
，v=
（2分）
由v=知，
=
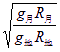（1分）
将R月=R地，g月=g地代入计算，可知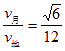
（≈0.2）（2分）
即近月卫星的运行速度约为近地卫星运行速度的
（0.2）倍．
解析:
在利用万有引力定律解决天体运动的有关问题是，通常把天体运动看成匀速圆周运动，其需要的向心力就是天体之间相互作用的万有引力提供。
即 
练习册系列答案
相关题目
图示是我国的“探月工程”向月球发射一颗绕月探测卫星“嫦娥一号”过程简图．月球探测计划“嫦娥工程”预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备．设想我国宇航员随“嫦娥”号登月飞船绕月球飞行，飞船上备有以下实验仪器：
R地，g月= 
g地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？
R地，g月=
g地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？
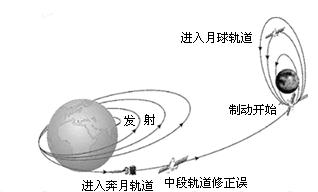
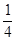R地，g月=
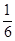g地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？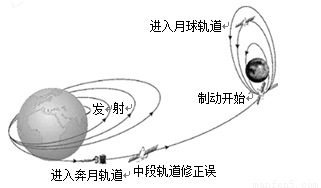
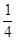R地，g月=
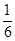g地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？