题目内容
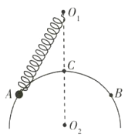
【题目】如图所示,轻弹簧一端固定在![]() 点,另一端系一小球,小球穿在固定于竖直面内、圆心为
点,另一端系一小球,小球穿在固定于竖直面内、圆心为![]() 的光滑圆环上,
的光滑圆环上,![]() 在
在![]() 的正上方,
的正上方,![]() 是
是![]() 的连线和圆环的交点,将小球从圆环上的
的连线和圆环的交点,将小球从圆环上的![]() 点无初速度释放后,发现小球通过了
点无初速度释放后,发现小球通过了![]() 点,最终在
点,最终在![]() 、
、![]() 之间做往复运动。已知小球在
之间做往复运动。已知小球在![]() 点时弹簧被拉长,在
点时弹簧被拉长,在![]() 点时弹簧被压缩,不计空气阻力,则下列判断正确的是( )
点时弹簧被压缩,不计空气阻力,则下列判断正确的是( )
A.弹簧在![]() 点的伸长量一定等于在
点的伸长量一定等于在![]() 点的压缩量
点的压缩量
B.小球从![]() 至
至![]() 一直做加速运动,从
一直做加速运动,从![]() 至
至![]() 一直做减速运动
一直做减速运动
C.弹簧处于原长时,小球的速度最大
D.小球机械能最大的位置有两处
【答案】D
【解析】
A.因只有重力和系统内弹力做功,故小球和弹簧组成的系统的机械能守恒,小球在![]() 点的动能和重力势能均最小,故小球在
点的动能和重力势能均最小,故小球在![]() 点的弹性势能必大于在
点的弹性势能必大于在![]() 点的弹性势能,所以弹簧在
点的弹性势能,所以弹簧在![]() 点的伸长量一定大于在
点的伸长量一定大于在![]() 点的压缩量,故A错误;
点的压缩量,故A错误;
BC.小球从![]() 至
至![]() ,先做加速运动再做减速运动,当所受合力为零(此时弹簧仍处于伸长状态)时,速度最大,故BC错误;
,先做加速运动再做减速运动,当所受合力为零(此时弹簧仍处于伸长状态)时,速度最大,故BC错误;
D.当弹簧处于原长时,弹性势能为零,小球机械能最大,由题意知,![]() 、
、![]() 相对于
相对于![]() 对称,显然,小球机械能最大的位置在
对称,显然,小球机械能最大的位置在![]() 、
、![]() 与
与![]() 、
、![]() 之间各有一处,故D正确。
之间各有一处,故D正确。
故选D。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目