题目内容
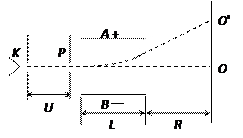
水平放置的两块平行金属板长L=5.0cm,两板间距d=1.0cm,两板间电压为90V,且上板为正,一个电子沿水平方向以速度v0=2.0×107m/s从两板中间射入,如图,求:(电子电量为-1.6×10-19C,质量为0.90×10-30kg)
(1)电子飞出电场时的侧移量是多少?
(2)电子飞出电场时的速度大小是多少?
(3)电子飞出电场时速度偏转角的正切值是多少?

(1)电子飞出电场时的侧移量是多少?
(2)电子飞出电场时的速度大小是多少?
(3)电子飞出电场时速度偏转角的正切值是多少?

由于电子在电场中所受电场力远大于电子所受重力作用,故本题中电子所受重力忽略不计.
(1)电子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动,故有:
水平方向:v0t=L,可得电子在电场中运动的时间为:t=
竖直方向:y=
at2=
?
?(
)2=
×
×(
)2m=5×10-3m
(2)电子飞出电场时,水平分速度vx=v0,竖直分速度:
vy=at=
?
=
m/s=4×106m/s
飞出电场时的速度为:v=
,
代入数据可得:v≈2.04×107m/s
(3)电子飞出电场时速度偏转角的正切值:tanθ=
=
=
答:(1)电子飞出电场时的侧移量是5×10-3m;
(2)电子飞出电场时的速度大小是2.04×107m/s;
(3)电子飞出电场时速度偏转角的正切值是
.
(1)电子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动,故有:
水平方向:v0t=L,可得电子在电场中运动的时间为:t=
| L |
| v0 |
竖直方向:y=
| 1 |
| 2 |
| 1 |
| 2 |
| qU |
| md |
| L |
| v0 |
| 1 |
| 2 |
| 1.6×10-19×90 |
| 0.9×10-30×1×10-2 |
| 5×10-2 |
| 2×107 |
(2)电子飞出电场时,水平分速度vx=v0,竖直分速度:
vy=at=
| qU |
| md |
| L |
| v0 |
| 1.6×10-19×90×0.05 |
| 0.9×10-30×0.01×2×107 |
飞出电场时的速度为:v=
|
代入数据可得:v≈2.04×107m/s
(3)电子飞出电场时速度偏转角的正切值:tanθ=
| vy |
| vx |
| 4×106 |
| 2×107 |
| 1 |
| 5 |
答:(1)电子飞出电场时的侧移量是5×10-3m;
(2)电子飞出电场时的速度大小是2.04×107m/s;
(3)电子飞出电场时速度偏转角的正切值是
| 1 |
| 5 |

练习册系列答案
相关题目