��Ŀ����
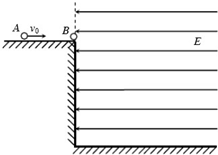 ��ͼ��ʾ��һ���⻬����Եˮƽ��̨������ռ��д��ڷ�Χ�㹻����ˮƽ�������ǿ�糡����̨��Ե����һ��������Ϊ+q������Ϊm��С��B������һ����Ե�������С��A����С��С��B��ͬ����������m���Գ��ٶ�v0��B�˶���A��B����������ײ��ˮƽ����糡�������ٴ���ײ���䵽ˮƽ���森��֪��ǿ�糡�ĵ糡��ǿΪE=
��ͼ��ʾ��һ���⻬����Եˮƽ��̨������ռ��д��ڷ�Χ�㹻����ˮƽ�������ǿ�糡����̨��Ե����һ��������Ϊ+q������Ϊm��С��B������һ����Ե�������С��A����С��С��B��ͬ����������m���Գ��ٶ�v0��B�˶���A��B����������ײ��ˮƽ����糡�������ٴ���ײ���䵽ˮƽ���森��֪��ǿ�糡�ĵ糡��ǿΪE=| 2mg | q |
��1�����С��A������Ϊ3m����
��С��A��B����������ײ���״���ײ������Ե��ٶȣ�
��С��A��B�ٴ���ײǰ�˶����������������룻
��BС���ڵ糡����AС���ٴ���ײǰ���еĶ��ܣ�
��2���������B���������䣬�ı�A�������������������䣬A��BС���ٴ���ײǰ�˶����������������뼰�ٴ���ײ�����ĸ߶��Ƿ����仯����֤����Ľ��ۣ�
��������1����С��A��B����������ײ�Ĺ����ж����غ㡢�����غ㣬���ݶ����غ㶨�ɺͻ�е���غ㶨�����������Ե��ٶȴ�С��
��A���磬���Գ�ƽ̨����ƽ���˶�������ֱ�������������壬ˮƽΪ�����˶��� B������ֱ���������������˶�����ˮƽ����������ֱ�����˶����ٶ�����Ϊ�ϣ���������������ֱ�����˶������ͬ��ʼ�ձ�����ͬһ�߶ȣ�������ˮƽ�ٶ����ʱ�������Զ��Ҳ���������ʱ��t��������ˮƽ�����ϵ�λ�ƣ����ݶ��κ�����ֵ�ķ�����������룮
�������ٴ�����ʱ����ˮƽ�����ϵ�λ����ȣ������˶�ѧ��ʽ���������ʱ�䣬�Ӷ������ֱ������λ�ƣ����ݶ��ܶ������B�Ķ��ܣ�
��2���������B���������䣬�ı�A�������������������䣬���ݶ����غ㶨�ɺ������غ㶨���������������ٶ�֮����Ƿ���С��������йأ��Ӷ������˶�ѧ��ʽ�ж��ٴ���ײǰ�˶����������������뼰�ٴ���ײ�����ĸ߶��Ƿ����仯��
��A���磬���Գ�ƽ̨����ƽ���˶�������ֱ�������������壬ˮƽΪ�����˶��� B������ֱ���������������˶�����ˮƽ����������ֱ�����˶����ٶ�����Ϊ�ϣ���������������ֱ�����˶������ͬ��ʼ�ձ�����ͬһ�߶ȣ�������ˮƽ�ٶ����ʱ�������Զ��Ҳ���������ʱ��t��������ˮƽ�����ϵ�λ�ƣ����ݶ��κ�����ֵ�ķ�����������룮
�������ٴ�����ʱ����ˮƽ�����ϵ�λ����ȣ������˶�ѧ��ʽ���������ʱ�䣬�Ӷ������ֱ������λ�ƣ����ݶ��ܶ������B�Ķ��ܣ�
��2���������B���������䣬�ı�A�������������������䣬���ݶ����غ㶨�ɺ������غ㶨���������������ٶ�֮����Ƿ���С��������йأ��Ӷ������˶�ѧ��ʽ�ж��ٴ���ײǰ�˶����������������뼰�ٴ���ײ�����ĸ߶��Ƿ����仯��
����⣺��1����A��B����������ײ 3mv0=3mv1+mv2����
��3m
=
��3m
+
m
����
�����٢ڽ�� v2=
v0��v1=
v0
��A���磬���Գ�ƽ̨����ƽ���˶�������ֱ�������������壬ˮƽΪ�����˶��� B������ֱ���������������˶�����ˮƽ����������ֱ�����˶����ٶ�����Ϊ�ϣ���������������ֱ�����˶������ͬ��ʼ�ձ�����ͬһ�߶ȣ�xA=v1t����
xB=v2t-
axt2����
B����ˮƽ�����ϵļ��ٶ�Ϊ aBx=
=
=2g����
���ԣ��ڷ��й�����A��B�ľ���Ϊ��x=xB-xA=(v2-v1)t -gt 2=v0t -g
��x=-(
t -
)2+
���Ե�t1=
ʱ����x�����ֵΪ
���ٴη�����ײʱ��xA=xB����
�����ۢܢݢ�÷����ٴ���ײ��ʱ��t2=
��xA=
�ٴ���ײ����ƽ̨�ĸ߶�h=
gt22=
����
�ɶ��ܶ���mgh-EqxA=EB-
m
����
���EB=
m
��2���������B���������䣬�ı�A��������
A��B����������ײm1v0=m1v1+m2v2����
m1
=
m1
+
m2
����
���������v2-v1=v0����A��BС�������أ�
�����ڷ��й�����A��B�ľ���Ϊ��x=v0t/1-g
���е�t/1=
ʱ����x�����ֵΪ
��A��BС���ٴ���ײǰ�˶����������������벻�����ı䣮
ͬ�������ٴ���ײ��ʱ��ʼ��Ϊt2/=
�������ٴ���ײ����ƽ̨�ĸ߶�Ϊh=
gt22=
���������ı䣬���ٴ���ײ����һ���̶��߶ȣ�
�𣺣�1��С��A��B����������ײ���״���ײ������Ե��ٶ�Ϊ
v0��
v0��
С��A��B�ٴ���ײǰ�˶�����������������Ϊ
��
BС���ڵ糡����AС���ٴ���ײǰ���еĶ���EB=
m
��
��2��A��BС���ٴ���ײǰ�˶����������������뼰�ٴ���ײ�����ĸ߶Ȳ��ı䣮
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
�����٢ڽ�� v2=
| 3 |
| 2 |
| 1 |
| 2 |
��A���磬���Գ�ƽ̨����ƽ���˶�������ֱ�������������壬ˮƽΪ�����˶��� B������ֱ���������������˶�����ˮƽ����������ֱ�����˶����ٶ�����Ϊ�ϣ���������������ֱ�����˶������ͬ��ʼ�ձ�����ͬһ�߶ȣ�xA=v1t����
xB=v2t-
| 1 |
| 2 |
B����ˮƽ�����ϵļ��ٶ�Ϊ aBx=
| Eq |
| m |
| ||
| m |
���ԣ��ڷ��й�����A��B�ľ���Ϊ��x=xB-xA=(v2-v1)t -gt 2=v0t -g
| t | 2 |
��x=-(
| g |
| v0 | ||
2
|
| ||
| 4g |
���Ե�t1=
| v0 |
| 2g |
| ||
| 4g |
���ٴη�����ײʱ��xA=xB����
�����ۢܢݢ�÷����ٴ���ײ��ʱ��t2=
| v0 |
| g |
| ||
| 2g |
�ٴ���ײ����ƽ̨�ĸ߶�h=
| 1 |
| 2 |
| ||
| 2g |
�ɶ��ܶ���mgh-EqxA=EB-
| 1 |
| 2 |
| v | 2 2 |
���EB=
| 5 |
| 8 |
| v | 2 0 |
��2���������B���������䣬�ı�A��������
A��B����������ײm1v0=m1v1+m2v2����
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
���������v2-v1=v0����A��BС�������أ�
�����ڷ��й�����A��B�ľ���Ϊ��x=v0t/1-g
| t/ | 2 1 |
���е�t/1=
| v0 |
| 2g |
| ||
| 4g |
ͬ�������ٴ���ײ��ʱ��ʼ��Ϊt2/=
| v0 |
| g |
| 1 |
| 2 |
| ||
| 2g |
�𣺣�1��С��A��B����������ײ���״���ײ������Ե��ٶ�Ϊ
| 1 |
| 2 |
| 3 |
| 2 |
С��A��B�ٴ���ײǰ�˶�����������������Ϊ
| ||
| 4g |
BС���ڵ糡����AС���ٴ���ײǰ���еĶ���EB=
| 5 |
| 8 |
| v | 2 0 |
��2��A��BС���ٴ���ײǰ�˶����������������뼰�ٴ���ײ�����ĸ߶Ȳ��ı䣮
�����������ۺ������˶����غ㶨�ɡ������غ㶨�ɡ�ţ�ٵڶ������Լ��˶�ѧ��ʽ���ۺ��Խ�ǿ����ѧ��������Ҫ��ϸߣ��ǵ����⣮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ��һ���⻬��С������ǽ�ں�бľ��֮�䣬��бľ�����ֱ ǽ�ڵļнǦȽǻ�������ʱ���ȣ�90�㣩��������
��ͼ��ʾ��һ���⻬��С������ǽ�ں�бľ��֮�䣬��бľ�����ֱ ǽ�ڵļнǦȽǻ�������ʱ���ȣ�90�㣩�������� ��ͼ��ʾ��һ���⻬��ˮƽ������Բ��������ӣ����а�Բ�������ֱƽ���ڣ��뾶ΪR������Ϊm��С���ɾ�ֹ��ˮƽ���������´�C�������A����ϰ�Բ��С��ͨ���������ߵ�B��ǡ����ƽ���˶�������������ˮƽ�����ϵ�C�㣬��֪AC=AB=2R����Ħ�����ƣ� ��
��ͼ��ʾ��һ���⻬��ˮƽ������Բ��������ӣ����а�Բ�������ֱƽ���ڣ��뾶ΪR������Ϊm��С���ɾ�ֹ��ˮƽ���������´�C�������A����ϰ�Բ��С��ͨ���������ߵ�B��ǡ����ƽ���˶�������������ˮƽ�����ϵ�C�㣬��֪AC=AB=2R����Ħ�����ƣ� �� ��ͼ��ʾ��һ���⻬��ˮƽ���AB��⻬��Բ���BCD���ӣ�����Բ�������ֱƽ���ڣ��뾶ΪR��BΪ��͵㣬DΪ��ߵ㣬һ������Ϊm��С���Գ��ٶ�V0��AB�˶����պ���ͨ����ߵ�D��������
��ͼ��ʾ��һ���⻬��ˮƽ���AB��⻬��Բ���BCD���ӣ�����Բ�������ֱƽ���ڣ��뾶ΪR��BΪ��͵㣬DΪ��ߵ㣬һ������Ϊm��С���Գ��ٶ�V0��AB�˶����պ���ͨ����ߵ�D��������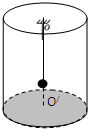 ��ͼ��ʾ��һ���⻬ԲͲ����ˮƽ�����ϣ�ԲͲ��ֱ��ΪL��һ������ҲΪL��ϸ��һ�˹̶���ԲͲ�������ϵ�O�㣬��һ��˩��һ������Ϊm��С����Ϊ�ʵ㣩��С��������v��������OO����ˮƽ����������Բ���˶�����������Ͳ�ף�����
��ͼ��ʾ��һ���⻬ԲͲ����ˮƽ�����ϣ�ԲͲ��ֱ��ΪL��һ������ҲΪL��ϸ��һ�˹̶���ԲͲ�������ϵ�O�㣬��һ��˩��һ������Ϊm��С����Ϊ�ʵ㣩��С��������v��������OO����ˮƽ����������Բ���˶�����������Ͳ�ף�����