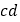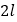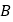题目内容
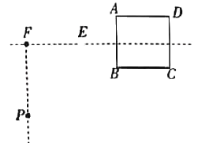
【题目】如图所示,一边长a=3m的正方体浮箱ABCD漂浮在水面上,恰好露出水面一半体积,AB边左侧水面上有不透明物体覆盖,但E处有一小孔,在E的左侧F处有一潜水员(视为质点)竖直向下潜水,当潜水员下潜到P处时恰好能从E处小孔看到浮箱上的A点。现测得E、F间距离s=3m。P、F间距离h=4m,已知水的折射率n=![]() 。
。
(i)求E点到AB的距离;
(ii)若浮箱向左移动s1=1m,求潜水员能从E处小孔看到浮箱的A点潜水的深度。(结果可保留根式)
【答案】(i)2m(ii)![]() m
m
【解析】
(i)从水中P点到A点的光路如图所示:

设E点到AB的距离为x,从P点看到A点时:
入射角的正弦值
sini=
折射角的正弦值
sinr=![]()
由折射定律可知:
n=![]()
解得:
x=2m
(ii)浮箱向左移动sl=l m时,A点移动到A′位置,则有
入射角的正弦值
sini′=
折射角的正弦值
sinr′=![]()
由折射定律可知:
n=![]()
解得:
h′=![]() m
m

练习册系列答案
相关题目