题目内容
【题目】如图所示，坐标系xoy在竖直平面内，空间有沿水平方向垂直于纸面向外的匀强磁场，磁感应强度大小为B，在x>0的空间里有沿x轴正方向的匀强电场，场强的大小为E，一个带正电的小球经过图中x轴上的A点，沿着与水平方向成θ=30°角的斜向下直线做匀速运动，经过y轴上的B点进入x<0的区域，要使小球进入x<0区域后能在竖直面内做匀速圆周运动，需在x<0区域内另加一匀强电场。若带电小球做圆周运动通过x轴上的C点，且OA=OC，设重力加速度为g，求：
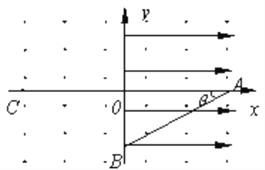
(1)小球运动速率的大小。
(2)在x<0的区域所加电场大小和方向。
(3)小球从B点运动C点所用时间及OA的长度。
【答案】(1)v=2E/B (2) 
方向竖直向上 (3)油滴从B运动到C的时间为
【解析】试题分析：(1）小球从A运动到B的过程中，小球受重力、电场力和洛伦兹力作用而处于平衡状态，
由题设条件知
，
所以小球的运动速率为
。
(2)小球在x<0的区域做匀速圆周运动，则小球的重力与所受的电场力平衡，洛伦兹力提供做圆周运动的向心力．
则
，
又
．
所以
，方向竖直向上．
(3）如图所示，连接BC，过B作AB的垂线交x轴于
．
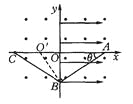
因为
，所以在
中
,又
，故
，所以
,
，则为小球做圆周运动的圆心．
设小球做圆周运动的半径为R,周期为T，则
,
且
，
由于
，小球从点B运动到点C的时间为
，
又∠BO=300，所以
,
所以
，
即
又
，
所以
练习册系列答案
相关题目
