题目内容
11.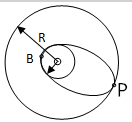 飞船沿半径为R的圆形轨道3绕地球做匀速圆周运动,周期为T,若飞船要返回地面,可在轨道上某点P处将速率降到适当的数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切.已知地球的质量为M,半径为R0,引力为G.求:
飞船沿半径为R的圆形轨道3绕地球做匀速圆周运动,周期为T,若飞船要返回地面,可在轨道上某点P处将速率降到适当的数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切.已知地球的质量为M,半径为R0,引力为G.求:(1)飞船在圆形轨道上运动时间经过P点处的加速度大小.
(2)飞船由P点运动到B点所需要的时间.
分析 (1)飞船在P点时由万有引力产生加速度,根据万有引力公式求解;
(2)从P到B经过半个周期,根据开普勒行星运动定律求解在椭圆轨道上的周期从而求得时间.
解答 解:(1)根据万有引力产生加速度,根据牛顿第二定律有:
$G\frac{Mm}{{R}^{2}}=ma$
可得飞船在P点的加速度为:a=$\frac{GM}{{R}^{2}}$;
(2)根据题意得椭圆轨道的半长轴为:r=$\frac{R+{R}_{0}}{2}$.
根据开普勒第三定律得:$\frac{{R}^{3}}{{T}^{2}}=\frac{{r}^{3}}{T{′}^{2}}$,
因为r=$\frac{R+{R}_{0}}{2}$,
解得:T′=$\sqrt{(\frac{R+{R}_{0}}{2R})^{3}}T$
则飞船由A点到B点的运动时间为:t=$\frac{T}{2}$=$\frac{1}{2}\sqrt{(\frac{R+{R}_{0}}{2R})^{3}}T$
答:(1)飞船在圆形轨道上运动时间经过P点处的加速度大小为$\frac{GM}{{R}^{2}}$;
(2)飞船由P点运动到B点所需要的时间为$\frac{1}{2}\sqrt{(\frac{R+{R}_{0}}{2R})^{3}}T$.
点评 由题目的描述,飞船由P点到B点所需的时间应是椭圆轨道的半个周期.关键掌握开普勒第三定律,并能灵活运用

练习册系列答案
相关题目
2. 随着社会生产的发展,大型化工厂已越来越多,环境污染也越来越严重.为减少环境污染,技术人员在排污管末端安装了如图所示的流量计.该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口.在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧面分别固定有金属板作为电极.污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )
随着社会生产的发展,大型化工厂已越来越多,环境污染也越来越严重.为减少环境污染,技术人员在排污管末端安装了如图所示的流量计.该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口.在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧面分别固定有金属板作为电极.污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )
 随着社会生产的发展,大型化工厂已越来越多,环境污染也越来越严重.为减少环境污染,技术人员在排污管末端安装了如图所示的流量计.该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口.在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧面分别固定有金属板作为电极.污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )
随着社会生产的发展,大型化工厂已越来越多,环境污染也越来越严重.为减少环境污染,技术人员在排污管末端安装了如图所示的流量计.该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口.在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧面分别固定有金属板作为电极.污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )| A. | 若污水中正离子较多,则前表面比后表面电势高 | |
| B. | 若污水中负离子较多,则前表面比后表面电势高 | |
| C. | 污水中离子浓度越高,电压表的示数将越大 | |
| D. | 所测的污水流量Q与U成正比 |
19.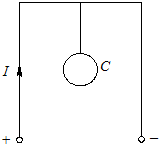 如图所示,一根长导线弯曲成“п”,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
如图所示,一根长导线弯曲成“п”,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
 如图所示,一根长导线弯曲成“п”,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
如图所示,一根长导线弯曲成“п”,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )| A. | 金属环中无感应电流产生 | B. | 金属环中有顺时针方向的感应电流 | ||
| C. | 悬挂金属环C的竖直线中拉力变大 | D. | 金属环C仍能保持静止状态 |
16.质量为m的木块从半径为R的半球形的光滑碗口下滑到碗的最低点的过程中,则( )


| A. | 初始时刻速度最小,所以木块的加速度为零 | |
| B. | 初始时刻速度最小,所以木块的加速度为g | |
| C. | 最低点时速度最大,木块的向心加速度最大 | |
| D. | 木块下滑过程中的向心加速度大小不变,方向时刻指向球心 |
3.(多选)当线圈中的磁通量发生变化时,下列说法中正确的是( )
| A. | 线圈中一定有感应电流 | |
| B. | 线圈中有感应电动势,其大小与磁通量成正比 | |
| C. | 线圈中一定有感应电动势 | |
| D. | 线圈中有感应电动势,其大小与磁通量的变化率成正比 |
 如图所示,ABC为一表面光滑的直角劈形物体,将其卡在孔中,斜边AB的长a=10cm直角边AC的长b=2cm,当用F=100N的力沿水平方向推物体时,求物体的上侧面和下侧面产生的推力大小.
如图所示,ABC为一表面光滑的直角劈形物体,将其卡在孔中,斜边AB的长a=10cm直角边AC的长b=2cm,当用F=100N的力沿水平方向推物体时,求物体的上侧面和下侧面产生的推力大小. 如图甲所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为l.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,导轨和金属杆的电阻可忽略.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下.让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦,重力加速度为g.
如图甲所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为l.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,导轨和金属杆的电阻可忽略.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下.让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦,重力加速度为g. 油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.6mL.用滴管向量筒内滴50滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成单分子油膜的形状如图所示.
油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.6mL.用滴管向量筒内滴50滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成单分子油膜的形状如图所示. AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求: