题目内容
5. 如图所示,在光滑的水平面上有A、B两个物体,A和B彼此紧靠在一起,A的上表面有一半径为R、顶端距水平面高为h的光滑半圆槽,槽顶有一可视为质点的小物体C,A、B、C三者质量均为m,现使物体C由静止沿槽下降,且运动过程中它始终与圆槽接触,求:
如图所示,在光滑的水平面上有A、B两个物体,A和B彼此紧靠在一起,A的上表面有一半径为R、顶端距水平面高为h的光滑半圆槽,槽顶有一可视为质点的小物体C,A、B、C三者质量均为m,现使物体C由静止沿槽下降,且运动过程中它始终与圆槽接触,求:(1)A和B刚分离时B的速度;
(2)A和B分离后,C能达到距水平面的最大高度.
分析 (1)A、B、C组成的系统在水平方向动量守恒,C到达圆弧低端时系统机械能守恒,由动量守恒定律与机械能守恒定律可以求出B的速度.
(2)A和B分离后,A与C水平方向的动量守恒,C达到距水平面的最大高度时,二者相对静止,结合机械能守恒定律即可求出.
解答 解:(1)C到达低端时,A、B分离,且A与B的速度相等,A、B、C系统在你水平方向动量守恒,以向左为正方向,在水平方向,由动量守恒定律得:
mvC-(m+m)vB=0,
系统机械能守恒,由机械能守恒定律得:$\frac{1}{2}$mvC2+$\frac{1}{2}$(m+m)vB2=mgR,
解得:vB=-$\sqrt{\frac{gR}{3}}$;负号表示方向向右
(2)A和B分离后,C达到距水平面的最大高度时,二者相对静止,对A、C系统水平方向的动量守恒,由动量守恒定律得:
mvC+mvB=(m+m)v,
设C到达的最大高度相对于槽低的高度为H,则由能量守恒定律得:$\frac{1}{2}$mvC2+$\frac{1}{2}$mvB2=$\frac{1}{2}$(m+m)v2+mgH,
解得:$H=\frac{3}{4}R$
所以C能达到距水平面的最大高度为:h′=h-(R-$\frac{3}{4}$R)=h-$\frac{1}{4}R$
答:(1)A和B刚分离时B的速度大小是$\sqrt{\frac{gR}{3}}$,方向向右;
(2)A和B分离后,C能达到距水平面的最大高度是h-$\frac{1}{4}R$.
点评 本题考查机械能守恒定律、动量守恒定律和能量守恒定律的应用.当球下落到最低点的过程,小球C与AB组成的系统机械能守恒.当球从最低点上升时,小球与槽组成的系统机械能守恒.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.关于粒子的说法,正确的是( )
| A. | 组成阴极射线的带电粒子是α粒子 | |
| B. | 卢瑟福在利用α粒子轰击氮原子核的实验中发现了质子 | |
| C. | 发生光电效应时,从金属表面逸出的粒子是光子 | |
| D. | 查德威克在利用α粒子轰击铍原子核的实验中发现了电子 |
20. 如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
 如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )| A. | M点处放置的是正电荷 | |
| B. | d点的电势高于f点的电势 | |
| C. | d点的场强与f点的场强相同 | |
| D. | 将带正电的试探电荷沿直线由d点移动到f点,电势能先增大后减小 |
14.如果取弹簧伸长△x时的弹性势能为0,则下列说法中正确的是( )
| A. | 弹簧处于原长时,弹簧的弹性势能为正值 | |
| B. | 弹簧处于原长时,弹簧的弹性势能为负值 | |
| C. | 当弹簧的压缩量为△x时,弹性势能的值为0 | |
| D. | 只要弹簧被压缩,弹性势能的值都为负值 |
15.下列说法正确的是( )
| A. | 将一块晶体敲碎后,得到的小颗粒是非晶体 | |
| B. | 固体可以分为晶体和非晶体两类,有些晶体在不同方向上有不同的光学性质 | |
| C. | 由同种元素构成的固体,可能会由于原子的排列方式不同而成为不同的晶体 | |
| D. | 在合适的条件下,某些晶体可以转变为非晶体,某些非晶体也可以转变为晶体 | |
| E. | 在熔化过程中,晶体要吸收热量,但温度保持不变,内能也保持不变 |
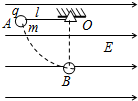 如图所示,在场强为E的匀强电场中,一绝缘轻质细杆l可绕点O点在竖直平面内自由转动,A端有一个带正电的小球,电荷量为q,质量为m.将细杆从水平位置自由释放,则:
如图所示,在场强为E的匀强电场中,一绝缘轻质细杆l可绕点O点在竖直平面内自由转动,A端有一个带正电的小球,电荷量为q,质量为m.将细杆从水平位置自由释放,则: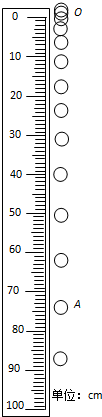 为验证小球在自由下落过程中机械能守恒,某实验小组进行了如下操作:
为验证小球在自由下落过程中机械能守恒,某实验小组进行了如下操作: