题目内容
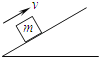
【题目】如图所示,光滑的倾斜轨道与半径为R的圆形轨道相连接,质量为m的小球在倾斜轨道上由静止释放,要使小球恰能通过圆形轨道的最高点,求:
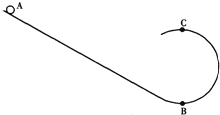
(1)通过轨道点最低点时球对轨道压力多大?
(2)小球释放点离圆形轨道最低点多高?
【答案】(1)6mg (2)2.5R
【解析】试题分析:由动能定理求出小球通过轨道最低点时的速度,在最低点,由合力提供向心力,由牛顿第二定律求出轨道对小球的支持力,从而得到小球对轨道的压力。
要使小球能够通过圆轨道的最高点,那么小球在最高点时,应该恰好由物体的重力作为向心力,由向心力的公式可以求得小球通过最高点的速度,再由机械能守恒可以求得释放点离地面的高度。
(1)小球恰能通过圆形轨道的最高点时,
有![]() ,得
,得![]()
令小球通过最低点的速度为vB,从B到C的过程,由机械能守恒定律得:
![]()
在最低点,由牛顿第二定律得: ![]()
由以上三式妥得:F=6mg.
由牛顿第三定律得小球对轨道的压力为:F′=F=6mg,方向竖直向下.
(2)从A到C的过程,由机械能守恒定律得:
![]()
由![]()
联立解得H=2.5R

练习册系列答案
相关题目