题目内容
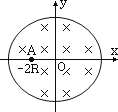
【题目】如图所示,在![]() 平面上,一个以原点
平面上,一个以原点![]() 为圆心,半径为
为圆心,半径为![]() 的圆形磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(
的圆形磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(![]() ,
,![]() )的
)的![]() 处静止着一个具有放射性的原子核氮——
处静止着一个具有放射性的原子核氮——![]() 。某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从
。某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从![]() 处射出时速度方向垂直于
处射出时速度方向垂直于![]() 轴,且后来通过了
轴,且后来通过了![]() 轴,而反冲核刚好不离开磁场区域。不计重力影响和离子间的相互作用。
轴,而反冲核刚好不离开磁场区域。不计重力影响和离子间的相互作用。
(1)写出衰变方程。
(2)求正电子做圆周运动的半径。
(3)求正电子最后过![]() 轴时的坐标。
轴时的坐标。
【答案】(1)![]() ;
;
(2);![]()
(3)![]()
【解析】
试题分析:(1)衰变方程为![]()
(2)设反冲核和正电子在磁场中回旋半径分别为![]() 、
、![]() ,由于反冲核与正电子都带正电荷,在磁场中的轨迹关系应是外切圆,因正电子通过
,由于反冲核与正电子都带正电荷,在磁场中的轨迹关系应是外切圆,因正电子通过![]() 轴,反冲核速度方向向上,正电子速度方向向下。(2分)
轴,反冲核速度方向向上,正电子速度方向向下。(2分)
故反冲核的半径![]()
衰变过程中遵循动量守恒![]()
又由于![]()
可得![]()
可得正电子做圆周运动的半径![]()
(3)由图可知正电子应在通过![]() 轴前飞出圆形磁场区域,出射点为
轴前飞出圆形磁场区域,出射点为![]() ,其轨迹圆心在磁场边界与
,其轨迹圆心在磁场边界与![]() 轴的交点
轴的交点![]() 处,过
处,过![]() 点做出射速度的反向延长线可交于磁场边界
点做出射速度的反向延长线可交于磁场边界![]() 点,且
点,且![]() 点在
点在![]() 轴上(1分),根据几何知识可得
轴上(1分),根据几何知识可得![]()
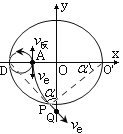
在直角三角形![]() 中,
中,![]()
因为![]() ,所以
,所以![]()
![]()
故正电子最后过![]() 轴的坐标为(
轴的坐标为(![]() )
)

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目