题目内容
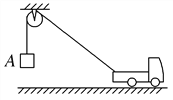
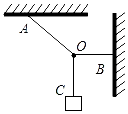
【题目】如图所示,半径R=0.3m的光滑圆弧轨道与粗糙斜面相切于B点,斜面最高点C距地面的高度h=0.15m,质量M=0.04kg的小物块从圆弧最低点A,以大小v=2m/s、方向向左的初速度开始运动,到斜面最高点C时速度为零.此时恰被从P点水平射出质量m=0.01kg弹丸击中,已知弹丸进人物块时速度方向沿着斜面,并立即停在物块内,P点距地面的高度H=1.95m弹丸的水平初速度v0=8m/s,取g=10m/s2.求:
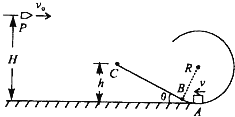
(1)斜面与水平地面的夹角θ;(可用反三角函数表示)
(2)物块回到A点时对轨道的压力大小;
(3)物块沿圆弧轨道运动,在所能到达的最高点处加速度大小.
【答案】(1)370(2)1.5N(3)10m/s2
【解析】(1)设弹丸做平抛运动的时间为t,则有:
![]()
解得:t=0.6s
此时弹丸的速度与水平方向夹角等于斜面倾角θ,竖直分速度为vy,则有:
vy=gt=6m/s
tanθ═vy/v0=3/4
∴θ=arctan3/4=37°
(2)设射入前子弹的速度为v1,则有: ![]()
子弹射入后,木块速度为v2,由动量守恒得:
mv1=(m+M)v2
解得:v2=2m/s
设物块与斜面的动摩擦因数为μ,斜面长为L,物块从A到C的过程中根据动能定理得:
mghμmgLcosθ=0![]()
物块从C到A的速度为v3,由能量守恒得:
(m+M)ghμ(m+M)gLcosθ=![]()
解得:v3=![]() m/s
m/s
设物块回到A点时轨道对它的支持力为N,由牛顿第二定律得: ![]()
解得:N=1.5N
(3)设物块在最高点处速度为零,距地面的高度为h1,由动能定理得: ![]()
解得:h1=0.3m=R
所以假设成立,轨道对物块无压力,物块只受重力作用,所以加速度为:
a=g=10m/s2

练习册系列答案
相关题目