��Ŀ����
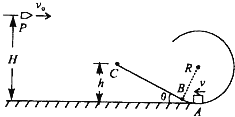
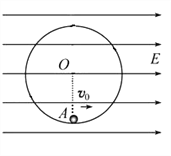
����Ŀ����ͼ��ʾΪ�̶�����ֱƽ���ڵģ��ڱڹ⻬�ľ�Ե�������뾶ΪR=1m��������ڵĿռ����ƽ���ڹ����ˮƽ���ҵ���ǿ�糡����ǿΪE=3��104N/C���ڹ�������¶�A����һ�������Ϊq=+2��10-4C������Ϊm=0.8kg��С���ָ�С��һ��ˮƽ���ҵij��ٶ�v0=4m/s��gȡ10m/s2����������ø�ʽ��ʾ����
��1��С�����˶����˲��Թ����ѹ�����
��2��С���˶�������ٶ��Ƕ��٣�
��3��ҪʹС�����˶������в�������������ٶ�v0Ҫ����ʲô������
���𰸡�(1)FN=20.8N��(2) ![]() ��(3)
��(3) ![]() ��
��![]()
�����������������(1)ͨ��Բ���˶�֪ʶ�ҵ�������������⣻
(2)���ö��ܶ���������⣻(3)����С�������������������һ����Ч�������е���ߵ㣬������Ч�������е�ˮƽλ�ã������ö��ܶ���������⣻
(1) ![]() ���ã�
���ã� ![]() ��
��
(2)�ɶ��ܶ����� ![]() �ã�
�ã� ![]() ��
��
(3) ��һ������� ![]()
![]()
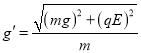
���ã� ![]() ��
��
�ڶ�������� ![]() �ã�
�ã� ![]() ��
��
���磺�������Ĺؼ����ҵ�������糡���ĵ�Ч�������ķ��������ö��ܶ�����⡣

��ϰ��ϵ�д�
�����Ŀ