题目内容
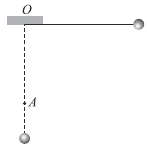
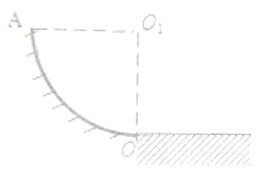
【题目】如图所示，AO为半径为R的1/4固定光滑圆周轨道，为O1圆心，O1A水平。一质量为m的小球从位置A静止释放，小球运动至最低点O的过程中，重力加速度为g，求：
（1）小球到达位置O时速度大小；
（2）当小球所在位置与O1的连线与O1A夹角为30°时，其重力的瞬时功率；
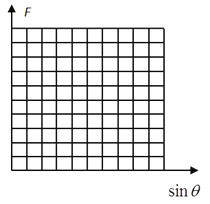
（3）假设小球所在位置与O1的连线与O1A夹角为
时，小球在上述过程中轨道对小球的作用力为F，试通过计算在坐标系中作出
图象。
【答案】（1）
（2）
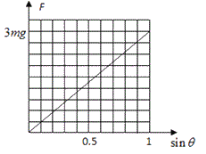
（3）
【解析】
（1）小球从A到O过程由动能定理有：
解得：
（2）当小球所在位置与O1的连线与O1A夹角为30°时，
由动能定理有：
此时重力的瞬时功率
解得：
（3）设小球所在位置与O1的连线与O1A夹角
时，有
在该处由牛顿第二定律有：
解得：
图象如图：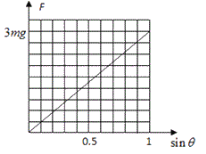
练习册系列答案
相关题目
